seychellesartprojects.org

Co je marginální výhoda?

Marginal Benefit pomáhá organizaci určit optimální úroveň výhody odvozené ze spotřeby a vypočítá odhadované množství jejího produktu / služby, které bude trh požadovat, čímž se zvýší nákladová efektivita při podnikání. Stručně řečeno, pomáhá organizaci efektivněji provozovat podnikání.

Mezní výhodou je postupné zvyšování ve prospěch spotřebitele v důsledku zvýšené spotřeby o další jednotku zakoupeného produktu nebo služby. Spokojenost spotřebitele má tendenci klesat s rostoucí spotřebou.

Formulace mezních výhod

Vzorec mezní výhody = změna v celkové výhodě / změna v počtu spotřebovaných jednotek

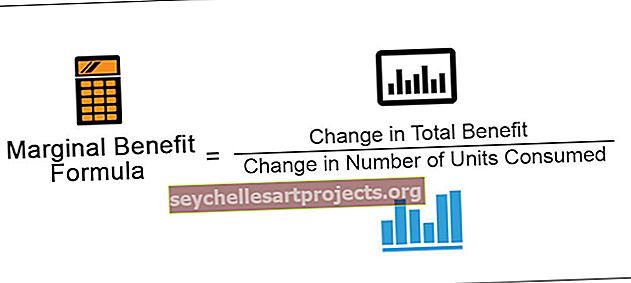
Změna celkových výhod

Tato část zahrnuje změnu celkového přínosu a je odvozena odečtením celkového přínosu aktuální spotřeby od předchozí spotřeby. Rozvíjíme lépe porozumění pomocí následujícího příkladu. Řekněme, že konzumací prvního banánu získá spotřebitel výhodu 10 jednotek, zatímco druhý banán vede k celkovému přínosu 18. Abychom dospěli ke změně celkové výhody mezi druhým a prvním banánem, musíme odečíst celkovou výhodu první banán z druhého banánu. Výsledkem je celková výhoda 8 (18 - 10).

Změna počtu spotřebovaných jednotek

Tato část zahrnuje výpočet změny v počtu spotřebovaných jednotek. Je odvozeno odečtením množství jednotky, která je aktuálně spotřebována, od dříve spotřebované jednotky. Změna jednotek spotřebovaných z druhého a prvního banánu je 1 (2 - 1).

Když jsou vypočítány obě části, je mezní výhoda odvozena vydělením změny v celkové výhodě rozdílem v počtu spotřebovaných jednotek.

Příklady

Tuto šablonu Excel s mezními výhodami si můžete stáhnout zde - Šablona Excel s mezními výhodami

Příklad č. 1

Předpokládejme, že spotřebitel, který Harry koupí a konzumuje zmrzlinu, nechť je výhoda plynoucí ze zmrzliny měřena jako 50 jednotek. Harry konzumuje další tři zmrzliny. Výhoda odvozená od 2., 3. a 4. zmrzliny je 40, 35 a 25. Vypočítejte okrajovou výhodu pro 1. a 2. a 1. a 3. jednotku zmrzliny.

Řešení:

Pro výpočet použijte uvedená data

Výpočet pro 1. a 2. zmrzlinu lze provést následovně:

1. a 2. zmrzlina je (50-40) / (2. - 1. jednotka)

Mezní výhoda pro 1. a 2. zmrzlinu = 10

Výpočet pro 3. a 1. zmrzlinu lze provést následovně:

Výhoda pro 3. a 1. zmrzlinu je (50 - 35) / (3. - 1. jednotka)

Výhoda pro 3. a 1. zmrzlinu bude -

Mezní výhoda pro 3. a 1. zmrzlinu = 7.5

Příklad č. 2

Pan Peter podniká v oblasti prodeje čaje. Na základě minulých prodejních zkušeností odhadl přínos plynoucí z konzumace svého čaje takto: 

Jste povinni vypočítat mezní výhodu pro každou prodanou jednotku navíc.

Řešení:

Okrajová výhoda pro množství jednoho čaje = (300-0) / (1-0)

Podobně můžeme vypočítat mezní přínos pro zbývající množství čaje.

Příklad č. 3

Řekněme, že pan Harry prodává zmrzlinu po 10 $. Variabilní náklady na výrobu jsou 5 $ za jednotku. To ponechává hrubý zisk 5 $ za jednotku. (Fixní náklady jsou pro jednoduchost ignorovány).

Řešení:

V neděli prodává 100 jednotek, což vede k hrubému zisku 5 x 100 jednotek nebo 500 $.

Ale kvůli zvýšení prodeje se Harry rozhodl snížit cenu na 9 $ každý. Za tuto cenu byste dosáhli hrubého zisku 4 $ za jednotku.

Kvůli sníženým cenám se objem prodeje zvýší na 180 jednotek. Prvních 100 spotřebitelů souhlasilo se zaplacením 10 USD, takže je ještě šťastnější, když zaplatili 9 USD. Dále se připojilo dalších 75 zákazníků, kteří jsou ochotni zaplatit 9 USD. Hrubý zisk je nyní 720.

Výpočet lze provést následujícím způsobem:

Mezní výhoda bude (720 $ - 500 $) / (180 jednotek - 100 jednotek)

Konečnou prodejní cenu může prodávající vypočítat na základě různých faktorů ovlivňujících jeho podnikání.

Relevance a použití

• Na základě optimální úrovně přínosu může organizace připravit rozpočet na množství, které má být vyrobeno.

Klíčové jídlo

• Změna počtu výhod odvozených zákazníkem zvýšením spotřeby o jednu další jednotku zboží / služby je okrajovým přínosem.
• Souvisí to nepřímo se spotřebou, tj. S nárůstem spotřeby klesá mezní užitek.
• Když se výroba nebo služba zvýší, změna nákladů, která vznikne, je mezními náklady na výrobu.
• Pomáhá při určování nejefektivnější úrovně požadovaných služeb nebo produktů.
• Pomáhá také dosáhnout úspor z rozsahu.