seychellesartprojects.org

Sharpe Ratio Definice

Sharpe ratio je poměr vyvinutý Williamem F. Sharpe a používaný investory za účelem odvození nadměrného průměrného výnosu portfolia nad bezrizikovou mírou výnosu na jednotku volatility (směrodatná odchylka) portfolia.

Vysvětlení

Sharpe Ratio je zásadní složkou pro stanovení celkové návratnosti portfolia. Jedná se o průměrný výnos vydělaný nad bezrizikový výnos ve srovnání s celkovou mírou neseného rizika. Jedná se o způsob, jak posoudit výkonnost investice úpravou její rizikové složky. Sharpeho poměr charakterizuje, jak dobře návratnost aktiva kompenzuje investora za přijaté riziko. Když porovnáváme dvě aktiva s běžnou referenční hodnotou, ta s vyšším Sharpeho poměrem je označena jako příznivá investiční příležitost se stejnou úrovní rizika.

Pokud se podíváte na výše uvedenou tabulku, uvidíte, že PRWCX má vyšší Sharpe Ratio 1,48 a je nejlepším fondem ve své skupině.

Sharpe Ratio, stejně jako jakýkoli jiný matematický model, spoléhá na přesnost údajů, která musí být správná. Při zkoumání investiční výkonnosti aktiv s vyhlazením výnosů by se Sharpeův poměr odvozoval spíše od výkonnosti podkladových aktiv než od výnosů fondu. Tento poměr se spolu s Treynor Ratios a Jeson's Alphas často používá k hodnocení výkonnosti různých portfolií nebo správců fondů.

Vzorec

V roce 1966 vytvořil William Sharpe tento poměr, který se původně nazýval poměrem „odměny k variabilitě“, než jej začali nazývat Sharpeův poměr následnými akademickými a finančními operátory. To bylo definováno několika způsoby, až nakonec to bylo mapováno jak dole:

Sharpe Ratio Formula = (očekávaný výnos - bezriziková míra návratnosti) / směrodatná odchylka (volatilita)

Některé z konceptů, které potřebujeme pochopit, jsou:

• Výnosy - Výnosy mohou mít různou frekvenci, například denní, týdenní, měsíční nebo roční, pokud se distribuce šíří normálně, protože tyto výnosy lze pro dosažení přesných výsledků anualizovat. Abnormální situace, jako jsou vyšší vrcholy, šikmost v distribuci, mohou být problémovou oblastí pro poměr, protože směrodatná odchylka nemá stejnou účinnost, pokud tyto problémy existují.
• Bezriziková míra návratnosti - Používá se k posouzení, zda je někdo správně kompenzován za dodatečné riziko, které nese kvůli rizikovému aktivu. Mírou návratnosti bez finanční ztráty jsou tradičně vládní cenné papíry s nejkratší dobou trvání (např. Americká státní pokladna). I když taková varianta cenného papíru vykazuje nejmenší volatilitu, lze tvrdit, že by se takové cenné papíry měly shodovat s jinými cennými papíry se stejnou dobou trvání.
• Standardní odchylka - je to veličina, která vyjadřuje, kolik jednotek z dané sady proměnných se liší od průměrného průměru skupiny. Jakmile je tento nadměrný výnos nad bezrizikovým výnosem vypočítán, musí být vydělen standardní odchylkou měřeného rizikového aktiva. Čím větší počet, tím atraktivnější bude investice z pohledu rizika / výnosu. Pokud však standardní odchylka není podstatně velká, páková složka nemusí mít na poměr vliv. Jak čitatel (návrat), tak jmenovatel (směrodatná odchylka) lze bez problémů zdvojnásobit.

Příklad

Klient „A“ v současné době drží 450 000 USD investovaných do portfolia s očekávaným výnosem 12% a volatilitou 10%. Efektivní portfolio má očekávaný výnos 17% a volatilitu 12%. Bezriziková úroková sazba je 5%. Co je Sharpe Ratio?

Sharpe Ratio Formula = (očekávaný výnos - bezriziková míra návratnosti) / směrodatná odchylka (volatilita)

Sharpe Ratio = (0,12-0,05) / 0,10 = 70% nebo 0,7x

Výpočet Sharpe Ratio v aplikaci Excel

Nyní, když víme, jak vzorec funguje, vypočítáme Sharpe Ratio v aplikaci Excel.

Krok 1 - Získejte výnosy v tabulkovém formátu

Prvním krokem je zajištění výnosů portfolia podílového fondu, který chcete analyzovat. Časové období může být měsíční, čtvrtletní nebo roční. Níže uvedená tabulka uvádí roční výnosy podílového fondu.

Krok 2 - Získejte podrobnosti o návratu bez rizika v tabulce

V této tabulce níže jsem učinil předpoklad, že bezrizikový výnos je 3,0% po dobu 15 let. Bezriziková sazba se však může každý rok měnit a toto číslo zde musíte uvést.

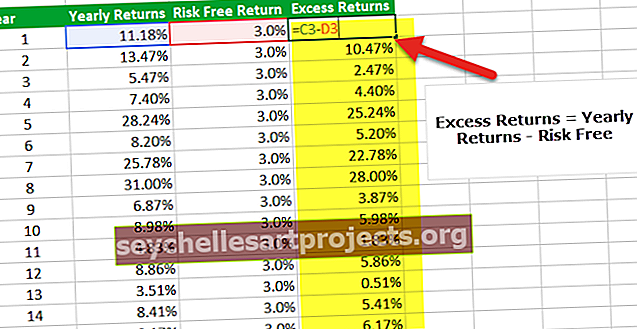
Krok 3 - Najděte nadměrný výnos

Třetím krokem při výpočtu Sharpe Ratio v aplikaci Excel je nalezení nadměrných výnosů portfolia. V našem případě je nadměrným výnosem roční výnos - bezrizikový výnos.

Krok 4 - Najděte průměr ročních výnosů.

Čtvrtým krokem při výpočtu Sharpe Ratio v Excelu je nalezení průměru ročních výnosů. Chcete-li najít průměr portfolia, můžete použít vzorec Excel PRŮMĚR. V našem příkladu získáme průměrný výnos 12,09%.

Krok 5 - Najděte standardní odchylku nadměrných výnosů

Chcete-li zjistit standardní odchylku nadměrných výnosů, můžete použít vzorec aplikace Excel STDEV, jak je uvedeno níže.

Krok 6 - Výpočet Sharpe Ratio

Posledním krokem k výpočtu Sharpeho poměru v aplikaci Excel je rozdělení průměrných výnosů standardní odchylkou. Získáme poměr = 12,09% / 8,8% = 1,37x

Získáme poměr = 12,09% / 8,8% = 1,37x

Výhody použití Sharpe Ratio

# 1 - Sharpe Ratio pomáhá při porovnávání a porovnávání přidávání nových aktiv

Používá se k porovnání rozptylu celkových funkcí portfolia rizik a výnosů, kdykoli je k němu přidáno nové aktivum nebo třída aktiv.

• Například správce portfolia zvažuje přidání alokace komoditního fondu do svého stávajícího investičního portfolia 80/20 akcií s Sharpeho poměrem 0,81.
• Pokud je alokace nového portfolia 40/40/20 akcií, dluhopisů a alokace dluhových fondů, Sharpe poměr se zvýší na 0,92.

To naznačuje, že ačkoliv je investice komoditního fondu volatilní jako samostatná expozice, v tomto případě ve skutečnosti vede ke zlepšení charakteristiky rizika a výnosu kombinovaného portfolia, a přináší tak výhodu diverzifikace do jiného aktiva třídy do stávajícího portfolia. Je třeba pečlivě analyzovat, že bude-li to mít negativní dopad na zdraví portfolia, bude možná v pozdější fázi muset být změněna alokace fondů. Pokud přidání nové investice vede ke snížení poměru, neměla by být do portfolia zahrnuta.

# 2 - Sharpe Ratio pomáhá při porovnávání návratnosti rizika

Tento poměr může také poskytnout vodítko k tomu, zda jsou nadměrné výnosy portfolia způsobeny pečlivým rozhodováním o investicích nebo výsledkem nepřiměřeného rizika. Přestože se jednotlivý fond nebo portfolio mohou těšit vyšším výnosům než jeho kolegové, je to pouze rozumná investice, pokud tyto vyšší výnosy nepřinášejí nepřiměřená rizika. Čím vyšší je Sharpeův poměr portfolia, tím lepší je jeho výkonnost při zohlednění rizikové složky. Záporný Sharpeho poměr naznačuje, že méně rizikové aktivum by fungovalo lépe než analyzované zabezpečení.

Vezměme si příklad srovnání rizik a výnosů.

Předpokládejme, že portfolio A mělo nebo se očekává 12% návratnost se standardní odchylkou 0,15. Za předpokladu srovnávacího výnosu asi 1,5% by míra návratnosti (R) byla 0,12, Rf bude 0,015 a 's' bude 0,15. Poměr bude čten jako (0,12 - 0,015) / 0,15, což znamená 0,70. Toto číslo však bude dávat smysl, když bude porovnáno s jiným portfoliem, jako je portfolio „B“

Pokud portfolio „B“ vykazuje větší variabilitu než portfolio „A“, ale má stejnou návratnost, bude mít větší standardní odchylku se stejnou mírou návratnosti z portfolia. Za předpokladu, že směrodatná odchylka pro Portfolio B je 0,20, bude rovnice čtena jako (0,12 - 0,015) / 0,15. Sharpov poměr pro toto portfolio bude 0,53, což je ve srovnání s portfoliem „A“ nižší. To nemusí být překvapivý výsledek, když vezmeme v úvahu skutečnost, že obě investice nabízejí stejný výnos, ale „B“ mělo větší kvantitu rizika. Je zřejmé, že ta, která má menší riziko nabídnout stejný výnos, bude upřednostňovanou možností.

Kritika Sharpe Ratio

Sharpeho poměr využívá standardní odchylku výnosů ve jmenovateli jako alternativu k celkovým rizikům portfolia, za předpokladu, že výnosy jsou rovnoměrně rozloženy. Předchozí testování ukázalo, že výnosy z určitých finančních aktiv se mohou lišit od normálního rozdělení, což má za následek zavádějící relevantní interpretace Sharpeho poměru.

Tento poměr lze zlepšit tím, že se různí správci fondů pokusí zvýšit jejich zdánlivý výnos upravený o riziko, což lze provést níže:

1. Prodloužení doby měření, která se má měřit : To povede k menší pravděpodobnosti volatility. Například anualizovaná standardní odchylka denních výnosů je obecně vyšší než týdenních výnosů, což je zase vyšší než u měsíčních výnosů. Čím delší je doba, tím jasnější je třeba vyloučit jakékoli jednorázové faktory, které mohou ovlivnit celkový výkon.
2. Složení měsíčních výnosů, ale výpočet směrodatné odchylky s vyloučením tohoto nedávno vypočítaného složeného měsíčního výnosu.
3. Zápis rozhodnutí portfolia o prodeji a koupi bez peněz: Taková strategie může potenciálně zvýšit výnosy výběrem prémie za opce, aniž by se několik let vyplácela. Strategie, které zahrnují zpochybnění rizika selhání, rizika likvidity nebo jiných forem široce se šířících rizik, mají stejnou schopnost vykazovat vzhůru předpojatý Sharpeův poměr.
4. Vyhlazení výnosů: Použití určitých derivátových struktur, nepravidelné oceňování méně likvidních aktiv na trhu nebo využití určitých cenových modelů, které podceňují měsíční zisky nebo ztráty, může snížit očekávanou volatilitu.
5. Eliminace extrémních výnosů: Příliš vysoké nebo příliš nízké výnosy mohou zvýšit vykazovanou standardní odchylku jakéhokoli portfolia, protože se jedná o vzdálenost od průměru. V takovém případě se správce fondu může rozhodnout, že každý rok eliminuje krajní (nejlepší a nejhorší) měsíční výnosy, aby snížil směrodatnou odchylku a ovlivnil výsledky, protože taková jednorázová situace může ovlivnit celkový průměr.

Ex-ante a ex-post Sharpe Ratio

Sharpeho poměr byl několikrát revidován, ale byly použity dvě obecné formy: ex-ante (predikce budoucího výnosu a rozptylu) a ex-post (analýza rozptylu z minulého výnosu).

• Předpovědi Sharpeho poměru ex-ante lze snadno odhadnout podle pozorování minulých výkonů podobných investičních aktivit.
• Ex-post Sharpe Ratio měří, jak vysoké byly výnosy, oproti tomu, jak různé byly tyto výnosy za dané časové období. Přesněji řečeno, je to poměr rozdílových výnosů (rozdíl mezi návratností investic a srovnávací investicí) versus historická variabilita (směrodatná odchylka) těchto výnosů.

Závěr

Sharpeho poměr je standardním měřítkem výkonnosti portfolia. Díky své jednoduchosti a snadné interpretaci je jedním z nejpopulárnějších indexů. Většina uživatelů bohužel zapomíná na předpoklady, které vedou k nevhodnému výsledku. Než se rozhodnete na trhu, měli byste zvážit kontrolu distribuce výnosů nebo ověření výsledků pomocí ekvivalentních měřítek výkonu.