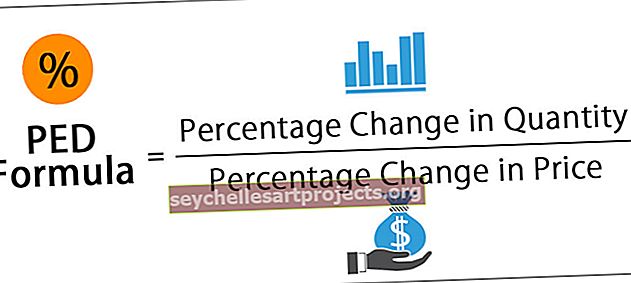seychellesartprojects.org

Co je testování hypotéz ve statistice?

Testování hypotéz odkazuje na statistický nástroj, který pomáhá měřit pravděpodobnost správnosti výsledku hypotézy, který je odvozen po provedení hypotézy na vzorových datech populace, tj. Potvrzuje, že to, zda byly odvozené výsledky primárních hypotéz správné, nebo ne.

Například pokud věříme, že výnosy z akciového indexu NASDAQ nejsou nulové. Nulovou hypotézou v tomto případě tedy je, že výnos z indexu NASDAQ je nulový.

Vzorec

Dvěma důležitými částmi jsou nulová hypotéza a alternativní hypotéza. Vzorec pro měření nulové hypotézy a alternativní hypotézy zahrnuje nulovou hypotézu a alternativní hypotézu.

H0: µ0 = 0

Ha: µ0 ≠ 0

Kde

• H0 = nulová hypotéza
• Ha = alternativní hypotéza

Budeme také muset vypočítat statistiku testu, abychom mohli odmítnout testování hypotézy.

Vzorec pro statistiku testu je znázorněn následovně,

T = µ / (s / √n)

Podrobné vysvětlení

Má dvě části, jedna je známá jako nulová hypotéza a druhá jako alternativní hypotéza. Nulová hypotéza je ta, kterou se výzkumník snaží odmítnout. Je obtížné dokázat alternativní hypotézu, takže pokud je nulová hypotéza odmítnuta, zbývající alternativní hypotéza bude přijata. Je testován na jiné úrovni významnosti pomocí výpočtu statistik testu.

Příklady

Tuto šablonu pro testování hypotéz Excel si můžete stáhnout zde - Šablona pro testování hypotéz Excel

Příklad č. 1

Pokusme se pochopit koncept testování hypotéz pomocí příkladu. Předpokládejme, že chceme vědět, že průměrný výnos z portfolia za období 200 dnů je větší než nula. Průměrná denní návratnost vzorku je 0,1% a standardní odchylka je 0,30%.

V tomto případě je nulovou hypotézou, kterou by výzkumník chtěl odmítnout, že průměrná denní návratnost portfolia je nulová. Nulová hypotéza je v tomto případě dvoustranný test. Budeme schopni odmítnout nulovou hypotézu, pokud je statistika mimo rozsah úrovně významnosti.

Při 10% hladině významnosti bude hodnota z pro dvoustranný test +/- 1,645. Pokud je tedy statistika testu mimo tento rozsah, hypotézu odmítneme.

Na základě uvedených informací určete statistiku testu

Výpočet statistiky testu bude tedy následující,

T = µ / (s / √n)

= 0,001 / (0,003 / √200)

Statistika testu bude -

Statistika testu je = 4,7

Vzhledem k tomu, že hodnota statistiky je více než +1 645, bude nulová hypotéza odmítnuta pro 10% hladinu významnosti. Proto je pro výzkum přijata alternativní hypotéza, že průměrná hodnota portfolia je větší než nula.

Příklad č. 2

Pokusme se pochopit koncept testování hypotéz pomocí dalšího příkladu. Předpokládejme, že chceme vědět, že střední výnos z podílového fondu za 365 dní je větší než nula. Průměrný denní výnos vzorku, pokud je 0,8%, a směrodatná odchylka je 0,25%.

V tomto případě je nulovou hypotézou, kterou by výzkumník chtěl odmítnout, že průměrná denní návratnost portfolia je nulová. Nulová hypotéza je v tomto případě dvoustranný test. Budeme schopni odmítnout nulovou hypotézu, pokud je statistika testu mimo rozsah úrovně významnosti.

Při 5% hladině významnosti bude hodnota z pro dvoustranný test +/- 1,96. Pokud je tedy statistika testu mimo tento rozsah, hypotézu odmítneme.

Níže jsou uvedena data pro výpočet statistik zkoušek

Výpočet statistiky testu bude tedy následující,

T = µ / (s / √n)

= 0,008 / (0,25 / √365)

Statistika testu bude -

Statistika testu = 61,14

Jelikož je hodnota testovací statistiky větší než +1,96, bude nulová hypotéza odmítnuta pro 5% hladinu významnosti. Proto je pro výzkum přijata alternativní hypotéza, že průměrná hodnota portfolia je větší než nula.

Příklad č. 3

Pokusme se pochopit koncept testování hypotéz pomocí jiného příkladu pro jinou úroveň významnosti. Předpokládejme, že chceme vědět, že průměrný výnos z portfolia opcí za 50denní období je větší než nula. Průměrný denní výnos vzorku je 0,13% a směrodatná odchylka je 0,45% .

V tomto případě je nulovou hypotézou, kterou by výzkumník chtěl odmítnout, že průměrná denní návratnost portfolia je nulová. Nulová hypotéza je v tomto případě dvoustranný test. Budeme schopni odmítnout nulovou hypotézu, pokud je statistika testu mimo rozsah úrovně významnosti.

Při 1% hladině významnosti bude hodnota z pro dvoustranný test +/- 2,33. Pokud je tedy statistika testu mimo tento rozsah, hypotézu odmítneme.

Následující údaje použijte pro výpočet statistiky testu

Výpočet statistiky testu lze provést takto -

T = µ / (s / √n)

= 0,0013 / (0,0045 / √50)

Statistika testu bude -

Statistika testu je = 2,04

Vzhledem k tomu, že hodnota testovací statistiky je menší než +2,33, nelze nulovou hypotézu pro úroveň významnosti 1% odmítnout. Proto je pro výzkum odmítnuta alternativní hypotéza, že průměrná hodnota portfolia je větší než nula.

Relevance a použití

Jedná se o statistickou metodu prováděnou za účelem testování konkrétní teorie a má dvě části, z nichž jedna je známá jako nulová hypotéza a druhá jako alternativní hypotéza. Nulová hypotéza je ta, kterou se výzkumník snaží odmítnout. Je obtížné dokázat alternativní hypotézu, takže pokud je nulová hypotéza odmítnuta, zbývající alternativní hypotéza bude přijata.

Je to velmi důležitý test k ověření teorie. V praxi je obtížné statisticky validovat teorii, proto se výzkumný pracovník snaží odmítnout nulovou hypotézu, aby ověřil alternativní hypotézu. Hraje důležitou roli při přijímání nebo odmítání rozhodnutí v podnicích.