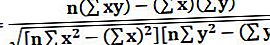Pearsonův korelační koeficient (vzorec, příklad) | Vypočítejte Pearson R.
Definice Pearsonova korelačního koeficientu
Pearsonův korelační koeficient, známý také jako Pearsonův statistický test, měří sílu mezi různými proměnnými a jejich vztahy. Kdykoli se mezi těmito dvěma proměnnými provádí statistický test, pak je vždy vhodné, aby osoba provádějící analýzu vypočítala hodnotu korelačního koeficientu, aby věděla, jak silný je vztah mezi těmito dvěma proměnnými.
Pearsonův korelační koeficient vrací hodnotu mezi -1 a 1. Interpretace korelačního koeficientu je následující:
- Pokud je korelační koeficient -1, znamená to silný negativní vztah. To znamená perfektní negativní vztah mezi proměnnými.
- Pokud je korelační koeficient 0, neznamená to žádný vztah.
- Pokud je korelační koeficient 1, znamená to silný pozitivní vztah. To znamená dokonalý pozitivní vztah mezi proměnnými.
Vyšší absolutní hodnota korelačního koeficientu naznačuje silnější vztah mezi proměnnými. Korelační koeficient 0,78 tedy naznačuje silnější pozitivní korelaci ve srovnání s hodnotou řekněme 0,36. Podobně korelační koeficient -0,87 naznačuje silnější negativní korelaci ve srovnání s korelačním koeficientem řekněme -0,40.

Jinými slovy, pokud je hodnota v kladném rozsahu, pak to ukazuje, že vztah mezi proměnnými je korelován pozitivně a obě hodnoty se společně snižují nebo zvyšují. Na druhou stranu, pokud je hodnota v záporném rozsahu, pak to ukazuje, že vztah mezi proměnnými je korelován negativně a obě hodnoty půjdou opačným směrem.
Vzorec Pearsonova korelačního koeficientu
Vzorec Pearsonova korelačního koeficientu je následující,


Kde,
- r = Pearsonův koeficient
- n = počet párů pažby
- ∑xy = součet produktů spárovaných akcií
- ∑x = součet skóre x
- ∑y = součet skóre y
- ∑x2 = součet čtverců x skóre
- ∑y2 = součet čtverců y skóre
Vysvětlení
Krok 1: Zjistěte počet párů proměnných, který je označen n. Předpokládejme, že x se skládá ze 3 proměnných - 6, 8, 10. Předpokládejme, že y se skládá z odpovídajících 3 proměnných 12, 10, 20.
Krok 2: Seznam proměnných ve dvou sloupcích.

Krok 3: Zjistěte součin xay ve 3. sloupci.

Krok 4: Zjistěte součet hodnot všech proměnných x a všech proměnných y. Výsledky zapište do spodní části 1. a 2. sloupce. Do 3. sloupce napište součet x * y.

Krok 5: Zjistěte x2 a y2 ve 4. a 5. sloupci a jejich součet ve spodní části sloupců.

Krok 6: Vložte do vzorce hodnoty nalezené výše a vyřešte to.
r = 3 * 352-24 * 42 / √ (3 * 200-242) * (3 * 644-422)
= 0,7559
Příklad Pearsonova korelačního koeficientu R
Tuto šablonu korelačního koeficientu Pearson Excel si můžete stáhnout zde - šablonu korelačního koeficientu Pearson ExcelPříklad 1
V tomto příkladu s pomocí následujících podrobností v tabulce 6 osob, které mají jiný věk a různé váhy uvedené níže pro výpočet hodnoty Pearson R

Řešení:
Pro výpočet Pearsonova korelačního koeficientu nejprve vypočítáme následující hodnoty,

Zde je celkový počet lidí 6, n = 6
Nyní je výpočet Pearson R následující,

- r = (n (∑xy) - (∑x) (∑y)) / (√ [n ∑x2- (∑x) 2] [n ∑y2– (∑y) 2)
- r = (6 * (13937) - (202) (409)) / (√ [6 * 7280 - (202) 2] * [6 * 28365- (409) 2)
- r = (6 * (13937) - (202) * (409)) / (√ [6 * 7280 - (202) 2] * [6 * 28365- (409) 2)
- r = (83622-82618) / (√ [43680-40804] * [170190-167281)
- r = 1004 / (√ [2876] * [2909)
- r = 1004 / (√ 8366284)
- r = 1004 / 2892,452938
- r = 0,35
Hodnota korelačního koeficientu Pearson je tedy 0,35
Příklad č. 2
Existují 2 akcie - A a B. Jejich ceny akcií v konkrétní dny jsou následující:

Zjistěte Pearsonův korelační koeficient z výše uvedených údajů.
Řešení:
Nejprve vypočítáme následující hodnoty.

Výpočet Pearsonova koeficientu je následující,

- r = (5 * 1935-266 * 37) / ((5 * 14298- (266) ^ 2) * (5 * 283- (37) ^ 2)) ^ 0,5
- = -0,9088
Proto je Pearsonův korelační koeficient mezi těmito dvěma zásobami -0,9088.
Výhody
- Pomáhá zjistit, jak silný je vztah mezi těmito dvěma proměnnými. Nejen přítomnost nebo nepřítomnost korelace mezi dvěma proměnnými je indikována pomocí Pearsonova korelačního koeficientu, ale také určuje přesný rozsah, v jakém tyto proměnné korelují.
- Pomocí této metody lze určit směr korelace, tj. Zda je korelace mezi dvěma proměnnými negativní nebo pozitivní.
Nevýhody
- Pearsonův korelační koeficient R nestačí k vyjádření rozdílu mezi závislými proměnnými a nezávislými proměnnými, protože korelační koeficient mezi proměnnými je symetrický. Například, pokud se člověk pokouší znát korelaci mezi vysokým stresem a krevním tlakem, mohl by najít vysokou hodnotu korelace, která ukazuje, že vysoký stres způsobuje krevní tlak. Nyní, pokud je proměnná přepnuta, bude výsledek v tom případě také stejný, což ukazuje, že stres je způsoben krevním tlakem, který nedává smysl. Výzkumník by si tedy měl být vědom dat, která používá k provádění analýzy.
- Pomocí této metody nelze získat informace o sklonu přímky, protože pouze uvádí, zda existuje nějaký vztah mezi těmito dvěma proměnnými nebo ne.
- Je pravděpodobné, že Pearsonův korelační koeficient může být nesprávně interpretován, zejména v případě homogenních údajů.
- Ve srovnání s ostatními metodami výpočtu trvá tato metoda, než se dospěje k výsledkům.
Důležité body
- Hodnoty se mohou pohybovat od hodnoty +1 po hodnotu -1, kde +1 označuje dokonalý pozitivní vztah mezi uvažovanými proměnnými, -1 označuje dokonalý negativní vztah mezi uvažovanými proměnnými a hodnota 0 označuje, že žádný vztah mezi uvažovanými proměnnými existuje.
- Je nezávislá na měrné jednotce proměnných. Pokud je například měrná jednotka jedné proměnné v letech, zatímco měrná jednotka druhé proměnné je v kilogramech, pak se hodnota tohoto koeficientu nezmění.
- Korelační koeficient mezi proměnnými je symetrický, což znamená, že hodnota korelačního koeficientu mezi Y a X nebo X a Y zůstane stejná.
Závěr
Pearsonův korelační koeficient je typ korelačního koeficientu, který představuje vztah mezi dvěma proměnnými, které se měří na stejném intervalu nebo stejné stupnici poměru. Měří sílu vztahu mezi dvěma spojitými proměnnými.
Uvádí nejen přítomnost nebo nepřítomnost korelace mezi těmito dvěma proměnnými, ale také určuje přesný rozsah, v němž jsou tyto proměnné korelovány. Je nezávislá na měrné jednotce proměnných, kde se hodnoty korelačního koeficientu mohou pohybovat od hodnoty +1 do hodnoty -1. Nestačí však poznat rozdíl mezi závislými proměnnými a nezávislými proměnnými.