seychellesartprojects.org

Klouzavý průměr znamená, že vypočítáme průměr průměrů souboru dat, který máme, v aplikaci Excel máme vestavěnou funkci pro výpočet klouzavého průměru, která je k dispozici na kartě Analýza dat v části Analýza, vyžaduje vstupní rozsah a výstup rozsah s intervaly jako výstupem, výpočty založené na pouhých vzorcích v aplikaci Excel pro výpočet klouzavého průměru jsou těžké, ale máme k tomu vestavěnou funkci v aplikaci Excel.

Co je klouzavý průměr v aplikaci Excel

Klouzavý průměr je široce používanou technikou v analýze časových řad, která se používá k předpovědi budoucnosti. Klouzavé průměry v časové řadě jsou v zásadě konstruovány na základě průměrů různých sekvenčních hodnot dat jiných časových řad.

Existují tři typy klouzavých průměrů, jmenovitě jednoduchý klouzavý průměr, vážený klouzavý průměr a exponenciální klouzavý průměr v aplikaci Excel.

# 1 - Jednoduchý klouzavý průměr v aplikaci Excel

Jednoduchý klouzavý průměr pomáhá při výpočtu průměru posledního počtu období datové řady. Předpokládejme ceny n období. Pak je jednoduchý klouzavý průměr uveden jako

Jednoduchý klouzavý průměr = [P1 + P2 + …………. + Pn] / n

# 2 - Vážený klouzavý průměr v aplikaci Excel

Vážený klouzavý průměr poskytuje vážený průměr posledních n období. Váha klesá s každým datovým bodem předchozího časového období.

Vážený klouzavý průměr = (Cena * váhový faktor) + (Cena předchozího období * váhový faktor-1)

# 3 - Exponenciální klouzavý průměr v aplikaci Excel

Je to podobné jako jednoduchý klouzavý průměr, který měří trendy za určité časové období. Zatímco jednoduchý klouzavý průměr vypočítá průměr daných dat, exponenciální klouzavý průměr přikládá větší váhu aktuálním datům.

Exponenciální klouzavý průměr = (K x (C - P)) + P

Kde,

• K = exponenciální vyhlazovací konstanta
• C = aktuální cena
• P = předchozí období exponenciální klouzavý průměr (jednoduchý klouzavý průměr používaný pro výpočet prvních období)

Jak vypočítat klouzavý průměr v aplikaci Excel?

Níže uvádíme příklad klouzavého průměru v aplikaci Excel.

Tuto šablonu aplikace Klouzavý průměr aplikace Excel si můžete stáhnout zde - Šablona aplikace Klouzavý průměr aplikace Excel

Příklad č. 1 - Jednoduchý klouzavý průměr v aplikaci Excel

Pro výpočet jednoduchého klouzavého průměru jsme vzali údaje o prodeji společnosti od ledna do prosince za rok 2018. Naším cílem je data vyhladit a znát údaje o prodeji v lednu 2019. Použijeme zde tříměsíční klouzavý průměr.

Krok 1:  Klouzavý průměr ledna, února a března se vypočítá tak, že se vezme součet prodejních čísel za měsíce a poté se vydělí 3.

Krok 2:  Výběrem v rohu buňky D5 a následným přetažením získáte klouzavý průměr pro zbývající období. Toto je funkce nástroje Excel pro vyplňování.

Předpověď prodeje na leden 2019 je 10456,66667.

Krok 3:  Nyní vykreslíme číslo prodeje a klouzavý průměr do spojnicového grafu, abychom porozuměli rozdílu v trendu. To lze provést na kartě vložení. Nejprve jsme vybrali datovou řadu a poté v sekci Grafy pod vložkou jsme použili spojnicový graf.

Po vytvoření grafů je vidět, že graf s klouzavým průměrem je mnohem vyhlazenější než původní datové řady.

Příklad č. 2 - Jednoduchý klouzavý průměr na kartě Analýza dat v aplikaci Excel

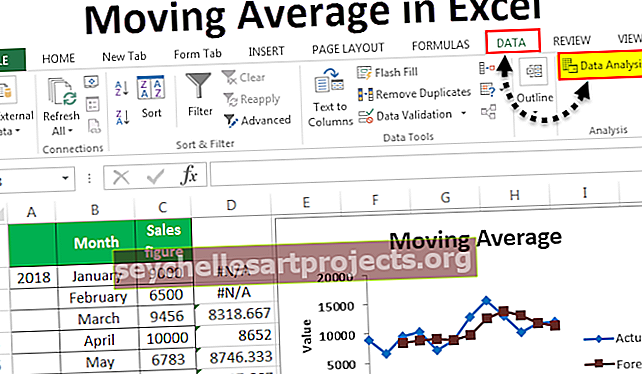
• Na kartě Data ve skupině Analýza musíme kliknout na Analýza dat. Následuje snímek obrazovky.

• Z analýzy dat lze získat klouzavý průměr.

• Po kliknutí na klouzavý průměr jsme jako vstupní rozsah vybrali údaj o prodeji.

• Na štítky v prvním řádku se klikne, aby aplikace Excel pochopila, že první řádek má název štítku.

• Interval 3 je vybrán proto, že chceme klouzavý průměr tří let.

• Vybrali jsme výstupní rozsah s přilnavostí k údaji o prodeji.

• Chceme také vidět výstup grafu, kde budeme moci vidět rozdíl mezi skutečným a předpovídaným.

Tento graf ukazuje rozdíl mezi skutečným a předpovídaným klouzavým průměrem.

Příklad č. 3 - Vážený klouzavý průměr v aplikaci Excel

Používáme tříletý vážený klouzavý průměr a vzorec je uveden na snímku obrazovky.

Po použití vzorce jsme dostali klouzavý průměr za období.

Klouzavý průměr pro všechna ostatní období jsme dostali přetažením hodnot v následujících buňkách.

Předpověď na leden 2019, tj. 10718,33

Nyní jsme vzali spojnicový graf, abychom viděli vyhlazení dat. Z tohoto důvodu jsme vybrali náš měsíc prognózovaná data a poté vložili spojnicový graf.

Nyní porovnáme naše prognózované údaje s našimi skutečnými údaji. Na níže uvedených screenshotech můžeme snadno vidět rozdíl mezi skutečnými a předpovídanými daty. Graf nahoře jsou skutečná data a graf níže je klouzavý průměr a prognózovaná data. Vidíme, že graf klouzavého průměru se významně vyhladil ve srovnání s grafem, který obsahuje skutečná data.

Příklad č. 4 - Exponenciální klouzavý průměr v aplikaci Excel

Vzorec pro exponenciální klouzavý průměr je  S _t = α.Y _t-1 + (1- α) S _t-1 …… (1)

Kde,

• Y _t-1 = skutečné pozorování v t-1. Období
• S _t-1 = jednoduchý klouzavý průměr v t-1. Období
• α = vyhlazovací faktor a pohybuje se mezi 0,1 a 0,3. Čím větší je hodnota α, tím blíže je graf skutečným hodnotám a čím menší je hodnota α, tím hladší bude graf.

Nejprve vypočítáme jednoduchý klouzavý průměr, jak je znázorněno výše. Poté použijeme vzorec uvedený v rovnici (1). Pro fixaci hodnoty α pro všechny následující hodnoty jsme stiskli F4.

Hodnoty získáme přetažením v následujících buňkách.

Nyní chceme vidět srovnání mezi skutečnými hodnotami, jednoduchým klouzavým průměrem a exponenciálním klouzavým průměrem v aplikaci Excel. Udělali jsme to provedením spojnicového grafu.

Na výše uvedeném snímku obrazovky vidíme rozdíl mezi skutečným prodejním číslem, jednoduchým klouzavým průměrem a exponenciálním klouzavým průměrem v aplikaci Excel.

Důležité informace o klouzavém průměru v aplikaci Excel

1. Jednoduchý klouzavý průměr lze vypočítat pomocí funkce PRŮMĚR v aplikaci Excel
2. Klouzavý průměr pomáhá při vyhlazení dat
3. Sezónní průměry se často označují jako sezónní index
4. Exponenciální klouzavý průměr v aplikaci Excel dává nedávným datům větší váhu než jednoduchý klouzavý průměr. Proto je vyhlazení v případě exponenciálního klouzavého průměru v aplikaci Excel více než u jednoduchého klouzavého průměru.
5. V podnicích, jako je akciový trh, klouzavý průměr pomáhá obchodníkovi snáze identifikovat trend.