seychellesartprojects.org

Vzorec pro výpočet návratnosti celkového portfolia

Vzorec pro návratnost portfolia se používá k výpočtu návratnosti celkového portfolia sestávajícího z různých jednotlivých aktiv, kde se podle vzorce vypočítá návratnost portfolia výpočtem návratnosti investic získaných z jednotlivých aktiv vynásobených jejich příslušnou váhovou třídou v celkovém portfoliu a sčítání všech výslednic dohromady.

Výnos portfolia lze definovat jako součet součinu výnosů z investic získaných u jednotlivého aktiva s váhovou třídou daného jednotlivého aktiva v celém portfoliu. Představuje návratnost portfolia a ne jednotlivého aktiva.

Očekávaný výnos lze vypočítat pomocí produktu potenciálních výsledků (tj. Výnosů, které jsou níže znázorněny r) váhami každého aktiva v portfoliu (tj. Představovanými w) a poté výpočtem součtu těchto výsledků.

R _p = ∑n _{i = 1} w _i r _i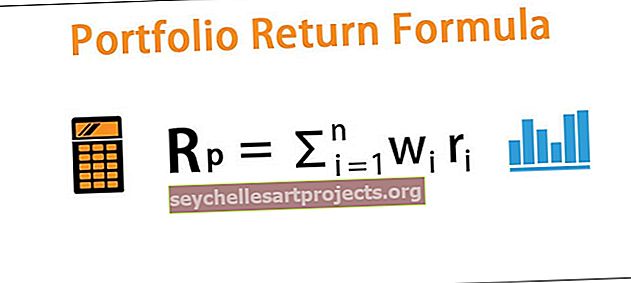

Kde ∑n _{i = 1} w _i = 1

• w je váha každého aktiva
• r je návratnost aktiva

Výpočet návratnosti portfolia (krok za krokem)

Výpočet návratnosti portfolia je poměrně jednoduchý, ale vyžaduje malou pozornost.

• Krok 1: Získejte výnosy z jednotlivých aktiv, do kterých byly fondy investovány. Například pokud investor investoval do vlastního kapitálu, je třeba vypočítat celý výnos, který je celkovým výnosem, včetně průběžných peněžních toků, které v případě akcií by byla dividenda.
• Krok 2: Vypočítejte váhy jednotlivého aktiva, do kterého jsou investovány finanční prostředky. Toho lze dosáhnout vydělením investované částky daného aktiva celkovým investovaným fondem.
• Krok 3: Vezměte produkt návratnosti, který se vypočítá v kroku 1, s váhou, která se vypočítá v kroku 2.
• Krok 4: Třetí krok se bude opakovat, dokud nebudou dokončeny výpočty všech aktiv. Nakonec musíme sečíst produkt všech jednotlivých výnosů aktiv podle jeho váhové třídy, kterou bude výnos portfolia.

Příklady

Tuto šablonu Excel pro návratovou formuli Excel si můžete stáhnout zde - Šablona Excel pro návratovou formuli portfolia

Příklad č. 1

Zvažte společnost ABC ltd, která společnost pro správu aktiv investovala do 2 různých aktiv spolu s jejich výnosem v loňském roce. Jste povinni získat návratnost portfolia.

Řešení:

Dostáváme individuální návratnost aktiv a spolu s touto investiční částkou, proto nejprve zjistíme váhy následujícím způsobem,

• Hmotnost (třída aktiv 1) = 1,00,000,00 / 1,50,000.00 = 0,67

Podobně jsme vypočítali váhu třídy aktiv 2

• Hmotnost (třída aktiv 1) = 50 000,00 / 1 500 000,00 = 0,33

Nyní pro výpočet návratnosti portfolia musíme vynásobit váhy návratností aktiva a poté tyto výnosy shrneme.

• W _i R _i (třída aktiv 1) = 0,67 * 10% = 6,67%

podobně jsme vypočítali W _i R _i pro třídu aktiv 2

• W _i R _i (třída aktiv 2) = 0,33 * 11%
• = 3,67%

Výpočet návratnosti portfolia je následující,

Návrat portfolia

Návratnost portfolia bude 10,33%

Příklad č. 2

JP Morgan pronásleduje jednu z největších společností v oblasti investičního bankovnictví a provedla několik investic v různých třídách aktiv. Předseda společnosti Dimon se zajímá o návratnost celkových investic provedených společností. Musíte vypočítat návratnost portfolia.

Řešení:

Jsme zde pouze s ohledem na nejnovější tržní hodnotu a neexistují žádné přímé výnosy. Nejprve tedy musíme vypočítat Návratnost jednotlivých aktiv.

Musíme odečíst částku investice od tržní hodnoty, abychom dosáhli nadměrného výnosu, a poté, co ji vydělíte částkou investice, přinese naše výnosy z jednotlivých aktiv.

Poznámka: Podrobný výpočet najdete v šabloně aplikace Excel.

Nyní máme individuální návratnost aktiv a spolu s touto investiční částkou a nyní zjistíme váhy pomocí výše investice a nikoli tržní hodnoty následujícím způsobem,

Váha akcií = 300000000/335600000 = 0,3966

Podobně jsme vypočítali váhu všech ostatních údajů.

Nyní pro výpočet návratnosti portfolia musíme vynásobit váhy návratností aktiva a poté tyto výnosy shrneme.

Výpočet návratnosti portfolia je následující,

Návrat portfolia

Výnos portfolia získaný společností JP Morgan je tedy 21,57%

Příklad č. 3

Gautam je jednotlivec, který nedávno začal investovat na trhu. Investoval do akcií XYZ za 100 000 a je to rok a od té doby obdržel dividendu 5 000 a aktuální tržní hodnota akcií XYZ se obchoduje s prémií 10%. Investoval také do fixního vkladu ve výši 20 000 a banka mu poskytuje 7% návratnost. A konečně investoval do půdy ve svém rodném městě za 500 000 a aktuální tržní hodnota je 700 000. Oslovil vás, aby vypočítal návratnost portfolia.

Řešení:

Jsme zde pouze s ohledem na nejnovější tržní hodnotu a neexistují žádné přímé výnosy. Nejprve tedy musíme vypočítat Návratnost jednotlivých aktiv.

Musíme odečíst částku investice od tržní hodnoty, abychom dosáhli nadměrného výnosu, a poté, co ji vydělíte částkou investice, přinese naše výnosy z jednotlivých aktiv.

Poznámka: Podrobný výpočet najdete v šabloně aplikace Excel.

Nyní máme individuální návratnost aktiv a spolu s touto investiční částkou a nyní zjistíme váhy pomocí výše investice, nikoli tržní hodnoty.

• Hmotnost (XYZ Stock) = 1,00,000 / 6,20,000 = 0,1613

Podobně jsme vypočítali váhu i pro další údaje.

Nyní pro výpočet návratnosti portfolia musíme vynásobit váhy návratností aktiva a poté tyto výnosy shrneme.

(XYZ Stock) W _i R _i = 0,15 * 0,1613 = 2,42%

Podobně jsme vypočítali W _i R _{i také} pro další konkrétní.

Výpočet návratnosti portfolia je následující,

Návrat portfolia

Výnos portfolia, který pan Gautam získal, je tedy 35,00%

Relevance a použití

Je zásadní chápat koncept vzorce očekávaného výnosu portfolia, protože stejný bude používán těmito investory, aby mohli předvídat zisk nebo ztrátu, které mohou nastat u fondů, které investují. Na základě tohoto vzorce očekávané návratnosti se může investor rozhodnout investovat do aktiva vzhledem k jejich pravděpodobným výnosům.

Investor bude dále schopen rozhodnout o váze aktiva v portfoliu, tj. Jaký podíl fondů by měl být investován, a poté provést požadovanou změnu.

Investor může také použít vzorec očekávaného výnosu pro hodnocení jednotlivých aktiv a dále případně může investovat prostředky podle hodnocení a poté je konečně zahrnout do svého portfolia. Jinými slovy by zvýšil váhu té třídy aktiv, jejíž očekávaný výnos je vyšší.