seychellesartprojects.org

Vzorec pro výpočet standardní směrodatné odchylky

Směrodatná odchylka vzorku odkazuje na statistickou metriku, která se používá k měření rozsahu, v jakém se náhodná proměnná odchyluje od průměru vzorku, a vypočítává se přidáním čtverců odchylky každé proměnné od průměru, poté výsledek vydělí počet proměnných minus a pak výpočet druhé odmocniny v excelu výsledku.

Matematicky je reprezentován jako,

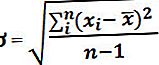
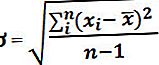
kde

• x _i = _i -ta náhodná proměnná
• X = průměr vzorku
• n = počet proměnných ve vzorku

Výpočet standardní směrodatné odchylky vzorku (krok za krokem)

• Krok 1: Nejprve shromážděte náhodné proměnné z populace velkého počtu proměnných. Tyto proměnné vytvoří vzorek. Proměnné jsou označeny x _i .
• Krok 2: Dále určete počet proměnných ve vzorku a je označen n.
• Krok 3: Dále určete průměr vzorku přidáním všech náhodných proměnných a vydělením výsledku počtem proměnných ve vzorku. Průměr vzorku je označen x.

• Krok 4: Dále vypočítejte rozdíl mezi každou proměnnou vzorku a střední hodnotou vzorku, tj. X _i - x.
• Krok 5: Dále vypočítáme druhou mocninu všech odchylek, tj. (X _i - x) 2.
• Krok 6: Dále přidejte všechny kvadratické odchylky, tj. ∑ (x _i - x) 2.
• Krok 7: Dále vydělte součet všech čtverců odchylek počtem proměnných ve vzorku mínus jedna tj. (N - 1).
• Krok 8: Nakonec se vzorec pro směrodatnou odchylku vzorku vypočítá výpočtem druhé odmocniny výše uvedeného výsledku, jak je uvedeno níže.

Příklady

Tuto vzorovou šablonu vzorové směrodatné odchylky vzoru Excel si můžete stáhnout zde - ukázkovou šablonu vzorové směrodatné odchylky vzoru Excel

Příklad č. 1

Vezměme si příklad vzorku 5 studentů, kteří byli dotazováni, abychom zjistili, kolik tužek každý týden používají. Vypočítejte směrodatnou odchylku vzorku na základě jejich daných odpovědí: 3, 2, 5, 6, 4

Vzhledem k tomu,

• Velikost vzorku (n) = 5

Níže jsou uvedena data pro výpočet směrodatné odchylky vzorku.

Průměr vzorku

Výpočet střední hodnoty vzorku

Průměr vzorku = (3 + 2 + 5 + 6 + 4) / 5

Průměr vzorku = 4

Čtverce odchylek každé proměnné lze vypočítat níže,

• (3 - 4) 2 = 1
• (2 - 4) 2 = 4
• (5 - 4) 2 = 1
• (6-4) 2 = 4
• (4 - 4) 2 = 0

Nyní lze standardní směrodatnou odchylku vypočítat pomocí výše uvedeného vzorce jako,

• ơ = √ {(1 + 4 + 1 + 4 + 0) / (5 - 1)}

Odchylka bude -

• ơ = 1,58

Proto je směrodatná odchylka vzorku 1,58.

Příklad č. 2

Vezměme si příklad kanceláře v New Yorku, kde pracuje přibližně 5 000 lidí, a byl proveden průzkum na vzorku 10 lidí ke stanovení průměrného věku pracující populace. Určete směrodatnou odchylku vzorku na základě věku 10 lidí: 23, 27, 33, 28, 21, 24, 36, 32, 29, 25

Vzhledem k tomu,

• Velikost vzorku (n) = 10

Použitím výše uvedených údajů nejprve vypočítáme průměr vzorku

Průměr vzorku

Výpočet střední hodnoty vzorku

= (23 + 27 + 33 + 28 + 21 + 24 + 36 + 32 + 29 + 25) / 10

Průměr vzorku = 27.8

Čtverce odchylek každé proměnné lze vypočítat níže,

• (23 - 27,8) 2 = 23,04
• (27 - 27,8) 2 = 0,64
• (33 - 27,8) 2 = 27,04
• (28 - 27,8) 2 = 0,04
• (21 - 27,8) 2 = 46,24
• (24 - 27,8) 2 = 14,44
• (36 - 27,8) 2 = 67,24
• (32 - 27,8) 2 = 17,64
• (29 - 27,8) 2 = 1,44
• (25 - 27,8) 2 = 7,84

Odchylka

Nyní lze odchylku vypočítat pomocí výše uvedeného vzorce jako,

• ơ = √ {(23,04 + 0,64 + 27,04 + 0,04 + 46,24 +14,44 +67,24 + 17,64 + 1,44 + 7,84) / (10 - 1)}

Odchylka bude -

• ơ = 4,78

Chcete-li porozumět podrobnému výpočtu, můžete se podívat na výše uvedený list aplikace Excel.

Relevance a použití

Koncept standardní směrodatné odchylky vzorku je z pohledu statistika velmi důležitý, protože obvykle se vzorek dat odebírá ze souboru velkých proměnných (populace), ze kterých se očekává, že statistik odhadne nebo zobecní výsledky pro celou populaci. Míra směrodatné odchylky není výjimkou a proto musí statistik provést vyhodnocení směrodatné odchylky populace na základě odebraného vzorku, a právě tam tato odchylka vstupuje do hry.