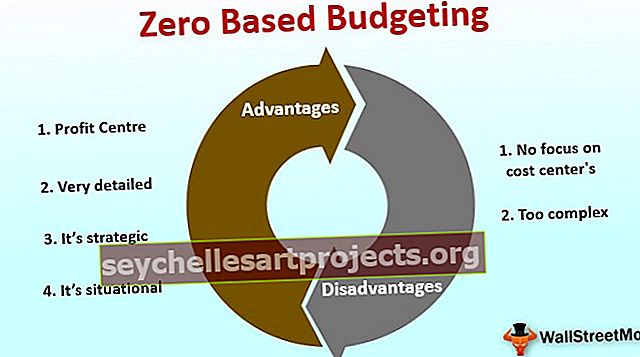
T Distribuční vzorec | Vypočítat rozdělení studentů T Příklad
Vzorec pro výpočet distribuce T studenta
Vzorec pro výpočet distribuce T (který je také populárně známý jako Studentova distribuce T) je zobrazen jako Odečtení průměrné hodnoty populace (průměr druhého vzorku) od průměrné hodnoty vzorku (průměr prvního vzorku), což je [x-bar - μ], které se potom vydělí směrodatnou odchylkou průměrů, která se zpočátku vydělí druhou odmocninou n, což je počet jednotek v daném vzorku [s ÷ √ (n)].
Distribuce T je druh distribuce, která vypadá téměř jako křivka normálního rozdělení nebo křivka zvonu, ale s trochu tlustším a kratším ocasem. Pokud je velikost vzorku malá, použije se místo normální distribuce tato distribuce.


Kde,
- x̄ je průměr vzorku
- μ je průměr populace
- s je směrodatná odchylka
- n je velikost daného vzorku
Výpočet rozdělení T
Výpočet distribuce t studentů je poměrně jednoduchý, ale ano, hodnoty jsou povinné. Například, jeden potřebuje populační průměr, což je vesmír znamená, což není nic jiného než průměr populace, zatímco výběrový průměr je vyžadován k testování autenticity populace, průměr, zda je tvrzení nárokované na základě populace skutečně pravdivé, a vzorek, pokud existuje bude představovat stejné prohlášení. Takže vzorec distribuce t zde odečte průměr vzorku od průměru populace a poté jej vydělí standardní odchylkou a vynásobí druhou odmocninou velikosti vzorku, aby se standardizovala hodnota.
Jelikož však neexistuje žádný rozsah pro výpočet t distribuce, hodnota může být divná a nebudeme moci vypočítat pravděpodobnost, protože distribuce t studenta má omezení z dosažení hodnoty, a proto je užitečná pouze pro menší velikost vzorku. Také pro výpočet pravděpodobnosti po dosažení skóre je třeba zjistit jeho hodnotu z distribuční tabulky studenta.
Příklady
Tuto šablonu T Distribution Excel si můžete stáhnout zde - Šablona T Distribution ExcelPříklad č. 1
Zvažte následující proměnné, které jste dostali:
- Průměr populace = 310
- Směrodatná odchylka = 50
- Velikost vzorku = 16
- Průměr vzorku = 290
Vypočítejte hodnotu t-rozdělení.
Řešení:
Následující údaje použijte pro výpočet distribuce T.

Výpočet distribuce T lze tedy provést následovně -
Zde jsou uvedeny všechny hodnoty, stačí je začlenit.
Můžeme použít t distribuční vzorec


Hodnota t = (290 - 310) / (50 / √16)

Hodnota T = -1,60
Příklad č. 2
Společnost SRH tvrdí, že její zaměstnanci na úrovni analytiků vydělávají v průměru 500 $ za hodinu. Je vybrán vzorek 30 zaměstnanců na úrovni analytiků a jejich průměrný výdělek za hodinu byl 450 $ s odchylkou vzorku 30 $ a za předpokladu, že jejich tvrzení je pravdivé, vypočítejte hodnotu t -distribuce, která se použije k nalezení pravděpodobnosti t - rozdělení.
Řešení:
Následující údaje použijte pro výpočet distribuce T.

Výpočet distribuce T lze tedy provést následovně -
Zde jsou uvedeny všechny hodnoty, stačí je začlenit.
Můžeme použít t distribuční vzorec


Hodnota t = (450 - 500) / (30 / √30)

Hodnota T = -9,13
Proto je hodnota skóre t -9,13
Příklad č. 3
Univerzitní školní rada administrovala test na úrovni IQ u 50 náhodně vybraných profesorů. A výsledkem, který z toho zjistili, bylo průměrné skóre úrovně IQ, bylo 120 s rozptylem 121. Předpokládejme, že skóre t je 2,407. Co znamená populace pro tento test, který by ospravedlnil hodnotu t skóre jako 2,407?
Řešení:
Následující údaje použijte pro výpočet distribuce T.

Zde jsou uvedeny všechny hodnoty spolu s hodnotou t, tentokrát musíme místo hodnoty t vypočítat průměrnou populaci.
Opět bychom použili dostupná data a vypočítáme průměr populace vložením hodnot uvedených ve vzorci níže.
Průměr vzorku je 120, průměr populace není znám, směrodatná odchylka vzorku bude druhá odmocnina rozptylu, která by byla 11 a velikost vzorku je 50.
Výpočet populačního průměru (μ) lze provést následujícím způsobem -
Můžeme použít t distribuční vzorec


Hodnota t = (120 - μ) / (11 / √50)
2,407 = (120 - μ) / (11 / √50)
-μ = -2,407 * (11 / √50) -120
Průměr populace (μ) bude -

μ = 116,26
Z tohoto důvodu bude hodnota pro průměrnou populaci 116,26
Relevance a použití
Distribuce T (a související hodnoty t skóre) se používá při testování hypotéz, když je potřeba zjistit, zda by měl odmítnout nebo přijmout nulovou hypotézu.

Ve výše uvedeném grafu bude centrální oblastí oblast přijímání a oblast ocasu bude oblastí odmítnutí. V tomto grafu, který je dvoustranným testem, bude modrá oblast odmítnutí. Oblast v oblasti ocasu lze popsat buď pomocí t-skóre, nebo pomocí z-skóre. Vezměte si příklad, obrázek vlevo bude zobrazovat oblast v ocasu pěti procent (což je 2,5% po obou stranách). Z-skóre by mělo být 1,96 (při převzetí hodnoty z tabulky z), což představuje 1,96 standardní odchylky od průměru nebo průměru. Nulovou hypotézu lze odmítnout, pokud je hodnota skóre z menší než hodnota -1,96 nebo je hodnota skóre z větší než 1,96.
Obecně se toto rozdělení použije tak, jak bylo popsáno dříve, pokud má člověk menší velikost vzorku (většinou pod 30) nebo pokud neví, jaká je odchylka populace nebo standardní odchylka populace. Z praktických důvodů (tj. Ve skutečném světě) by tomu tak vždy bylo. Pokud je velikost poskytovaného vzorku dostatečně velká, pak budou 2 distribuce prakticky podobné.