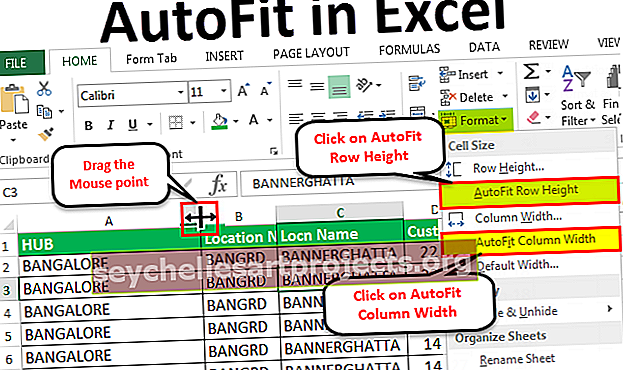
Histogramový vzorec | Výpočet plochy pomocí rovnice histogramu (příklady)
Histogram je typ grafického znázornění v aplikaci Excel a existuje několik způsobů, jak jej vytvořit, ale namísto použití analytických nástrojů nebo z kontingenční tabulky můžeme také vytvořit histogram ze vzorců a vzorce použité k vytvoření histogramu jsou FREQUENCY a Countifs vzorce společně.
Co je histogramový vzorec?
Vzorec pro histogram se v zásadě točí kolem oblasti pruhů a je velmi jednoduchý a vypočítává se součtem součinu frekvenční hustoty každého intervalu tříd a šířky odpovídajícího intervalu tříd. Oblast vzorce histogramu je matematicky znázorněna jako,


Vysvětlení vzorce histogramu
Vzorec pro výpočet plochy histogramu lze odvodit pomocí následujících jednoduchých sedmi kroků:
Krok 1 : Nejprve je třeba rozhodnout o tom, jak by měl být proces měřen a jaké údaje by měly být shromažďovány. Jakmile je rozhodnuto, data jsou shromážděna a prezentována v tabulkové formě, jako je tabulka.
Krok 2: Nyní spočítejte počet nasbíraných datových bodů.
Krok 3 : Dále určete rozsah vzorku, což je rozdíl mezi maximální a minimální hodnotou ve vzorku dat.
Rozsah = maximální hodnota - minimální hodnota
Krok 4: Dále určete počet intervalů tříd, které mohou být založeny na jedné z následujících dvou metod,
- Jako pravidlo palce použijte 10 jako počet intervalů nebo
- Počet intervalů lze vypočítat druhou odmocninou počtu datových bodů, která se poté zaokrouhlí na nejbližší celé číslo.
Počet intervalů = 
Krok 5: Nyní určete šířku třídy intervalů vydělením rozsahu datového vzorku počtem intervalů.
Šířka třídy = Rozsah / Počet intervalů
Krok 6: Dále vytvořte tabulku nebo tabulku s frekvencemi pro každý interval. Poté odvozte hustotu frekvence pro každý interval vydělením frekvence odpovídající šířkou třídy.
Krok 7: Nakonec se plocha pro rovnici histogramu vypočítá sečtením součinu veškeré frekvenční hustoty a jejich odpovídající šířky třídy.
Příklady vzorce histogramu (s šablonou aplikace Excel)
Podívejme se na jednoduchý a pokročilý příklad, abychom lépe porozuměli výpočtu rovnice histogramu.
Tuto šablonu Excel Histogram Formula si můžete stáhnout zde - Šablona Excel Histogram Formula
Histogramový vzorec - příklad č. 1
Uvažujme níže uvedenou tabulku, která ukazuje váhy dětí ve třídě.

Z výše uvedené tabulky lze vypočítat následující
- Šířka třídy prvního intervalu = 35 - 30 = 5
- Šířka třídy druhého intervalu = 45 - 35 = 10
- Šířka třídy třetího intervalu = 50 - 45 = 5
- Šířka třídy čtvrtého intervalu = 55 - 50 = 5
- Šířka třídy pátého intervalu = 65 - 55 = 10
Znovu,
- Hustota frekvence prvního intervalu = 2/5 = 0,4
- Hustota frekvence druhého intervalu = 7/10 = 0,7
- Hustota frekvence třetího intervalu = 21/5 = 4,2
- Hustota frekvence čtvrtého intervalu = 15/5 = 3,0
- Hustota frekvence pátého intervalu = 2/10 = 0,2
Pro výpočet vzorce histogramu nejprve budeme muset vypočítat šířku třídy a hustotu frekvence, jak je uvedeno výše.
Z toho důvodu, Oblast histogramu = 0,4 * 5 + 0,7 * 10 + 4,2 * 5 + 3,0 * 5 a 0,2 x 10

Takže oblast histogramu bude -

- Proto je oblast histogramu = 47 dětí
Grafické znázornění hmotnosti dětí je uvedeno níže,

Relevance a použití
Koncept rovnice histogramu je velmi užitečný, protože se používá k vykreslení sady dat. Ačkoli histogram vypadá docela podobně jako sloupcový graf, konečné použití histogramu je velmi odlišné od sloupcového grafu. Histogram je užitečný pro zobrazení většího množství dat srozumitelnějším způsobem, který lze snadno vizualizovat. Histogram zachycuje frekvenční hustotu každého intervalu třídy. Medián a distribuci dat lze určit z histogramu. Lze také určit nerovnost rozdělení, protože pruhy vlevo nebo vpravo jsou vyšší než to znamená, že data jsou zkosená nebo jinak jsou data symetrická.
Histogram nachází uplatnění především v případě rozsáhlých cvičení, jako je celostátní sčítání lidu, které lze provádět každých deset let. V takových případech jsou data shromážděna a uvedena v histogramu, aby je bylo možné snadno studovat. Také v případě průzkumů, kdy je vytvořen histogram, aby kdokoli, kdo je schopen interpretovat histogram, mohl později použít data pro další studie nebo analýzu.