seychellesartprojects.org

Co je to průběžné skládání?

Continuous Compounding vypočítá Limit, při kterém může Složený úrok dosáhnout neustálým složením na dobu neurčitou, čímž se zvýší úroková složka a nakonec hodnota portfolia celkových investic

Kontinuální skládací vzorec

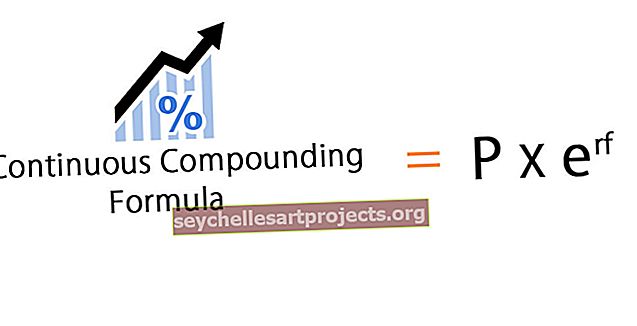
Kontinuální složený vzorec určuje získaný úrok, který je opakovaně složen na nekonečné časové období.

kde,

• P = jistina (současná hodnota)
• t = čas
• r = úroková sazba

Výpočet předpokládá konstantní složení během nekonečného počtu časových období. Protože časové období je nekonečné, exponent pomáhá při znásobení aktuální investice. To se vynásobí aktuální rychlostí a časem. Navzdory velkému počtu investic je rozdíl v celkovém úroku získaném díky kontinuálnímu složení excel menší ve srovnání s tradičním složením, na které se podíváme prostřednictvím příkladů.

Příklad

Pojďme analyzovat některé z případů:

Tuto šablonu aplikace Continuous Compounding Excel si můžete stáhnout zde - Šablona aplikace Continuous Compounding Excel

Pokud je počáteční investice ve výši 1 000 $ investována s 8% úrokem ročně s průběžným složením, kolik by bylo na účtu po 5 letech?

• P = 1 000 $, r = 8%, n = 5 let
• FV = P * e rt = 1 000 * e (0,08) (5) = 1 000 * e (0,40) [Exponent 0,4 je 1,491] = 1 000 * 1,491                                    
• = 1491,8 USD

Pojďme vypočítat účinky stejné na pravidelné složení:

Roční složení:

• FV = 1 000 * (1 + 0,08) ^ 1 = 1 080 USD

Pololetní složení:

• FV = 1 000 * [(1 + 0,08 / 2)] ^ 2   
• = 1 000 * (1,04) ^ 2   
• = 1 000 * 1,0816 =   1 081,60 USD

Čtvrtletní složení:

• FV = 1 000 * [(1 + 0,08 / 4)] ^ 4
• = 1 000 * (1,02) ^ 4
• = 1000 * 1,08243
• = 1 082,43 USD

Složení za měsíc:

• FV = 1 000 * [(1 + 0,08 / 12)] ^ 12
• = 1 000 * (1,006) ^ 4
• = 1 000 * 1,083
• = 1 083 $

Kontinuální skládání:

• FV = 1 000 * e 0,08
• = 1000 * 1,08328
• = 1 083,29 USD

Jak lze pozorovat z výše uvedeného příkladu, úrok získaný z nepřetržitého složení je 83,28 USD, což je jen o 0,28 USD více než měsíční složení.

Dalším příkladem může být spořicí účet, který platí 6% roční úrok, a to nepřetržitě. Kolik je nyní třeba investovat, aby na účtu bylo za 30 let 100 000 $?

• FV = PV * ert
• PV = FV * e - rt
• PV = 100 000 * e - (0,06) (30)
• PV = 100 000 * e - (1,80)
• PV = 100 000 * 0,165 2988
• PV = 16 529,89 USD

Pokud tedy dnes bude investována částka 16 530 USD (zaokrouhleno), přinese to po 30 letech při dané rychlosti 100 000 USD.

Další možností může být, pokud si půjčka účtuje 80% úrok, který je průběžně kombinován, jaká bude efektivní roční úroková sazba?

• Úroková sazba = e 0,80 - 1
• = 2,2255 - 1 = 1,22,55 = 122,55%

Použití

1. Spíše než neustálé skládání úroků na měsíční, čtvrtletní nebo roční bázi, bude to efektivně reinvestovat zisky neustále.
2. Účinek umožňuje reinvestovat částku úroku, což umožňuje investorovi vydělávat exponenciální rychlostí.
3. To určuje, že to nebude jen částka jistiny, která vydělá peníze, ale i průběžné skládání částky úroku se bude dále znásobovat.

Kontinuální skládací kalkulačka

Můžete použít následující kalkulačku

P
r
t
Kontinuální skládací vzorec =

Kontinuální skládací vzorec =	P xe (rxt) =
	0 * e (0 * 0) =	0

Kontinuální skládání vzorců v aplikaci Excel (se šablonou aplikace Excel)

To je velmi jednoduché. Musíte zadat dva vstupy: Základní částka, Čas a Úroková sazba.

Poměr můžete snadno vypočítat v poskytnuté šabloně.

Příklad - 1

Poměr můžete snadno vypočítat v poskytnuté šabloně.

Pojďme vypočítat účinky stejné na pravidelné složení:

Jak lze pozorovat na příkladu spojitého skládání, úrok získaný z tohoto složení je 83,28 USD, což je jen o 0,28 USD více než měsíční složení.

Příklad - 2

Příklad - 3