seychellesartprojects.org

Co je Harmonický průměr?

Harmonický průměr je převrácená hodnota aritmetického průměru převrácené hodnoty, tj. Průměr se vypočítá vydělením počtu pozorování v dané datové sadě součtem jejích vzájemných hodnot (1 / Xi) každého pozorování v dané datové sadě.

Harmonický střední vzorec

Harmonický průměr = n / ∑ [1 / X _i ]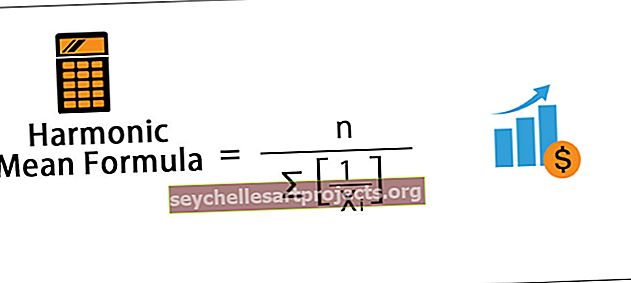

• Je vidět, že je to převrácená hodnota normálního průměru.
• Harmonický průměr pro normální průměr je ∑ x / n, takže pokud je vzorec obrácen, stane se n / ∑x a pak všechny hodnoty jmenovatele, které musí být použity, by měly být vzájemné, tj. Pro čitatele zůstává „n“, ale pro jmenovatel hodnot nebo pozorování pro ně musíme použít k převrácení hodnot.
• Hodnota, která je odvozena, by vždy byla nižší než průměr nebo řekla aritmetický průměr.

Příklady

Tuto šablonu Excel Harmonic Mean Formula si můžete stáhnout zde - Šablona Excel Harmonic Mean Formula

Příklad č. 1

Vezměme si datovou sadu následujících čísel: 10, 2, 4, 7. Pomocí výše diskutovaného vzorce musíte vypočítat harmonický průměr.

Řešení:

Pro výpočet použijte následující údaje.

Harmonický průměr = n / ∑ [1 / X _i ]

= 4 / (1/10 + 1/2 + 1/4 + 1/7)

= 4 / 0,99

Příklad č. 2

Mr.Vijay je analytik akcií v JP Morgan. Jeho manažer ho požádal, aby určil poměr P / E indexu, který sleduje ceny akcií společnosti W, společnosti X a společnosti Y. Společnost W vykazuje zisk 40 milionů USD a tržní kapitalizaci 2 miliardy USD, společnost X vykazuje zisk 3 miliardy dolarů a tržní kapitalizace 9 miliard dolarů a zatímco společnost Y uvádí zisk 10 miliard dolarů a tržní kapitalizaci 40 miliard dolarů. Vypočítejte harmonický průměr pro poměr P / E indexu.

Řešení:

Pro výpočet použijte následující údaje

Nejprve vypočítáme poměr P / E

Poměr P / E je v zásadě (tržní kapitalizace / zisk).

• P / E (společnost W) = (2 miliardy USD) / (40 milionů USD) = 50
• P / E společnosti (Company X) = (9 miliard USD) / (3 miliardy USD) = 3
• P / E (společnost Y) = (40 miliard USD) / (10 miliard USD) = 4

Výpočet hodnoty 1 / X

• Společnost W = 1/50 = 0,02
• Společnost X = 1/3 = 0,33
• Společnost Y = 1/4 = 0,25

Výpočet lze provést následujícím způsobem,

Harmonický průměr = n / ∑ [1 / X _i ]

• = 3 / (1/50 + 1/3 + 1/4)
• = 3 / 0,60

Příklad č. 3

Rey, obyvatel severní Kalifornie, je profesionální sportovní motorkář a v neděli večer kolem 17:00 východního času je na cestě ze svého domova na pláž. V první polovině cesty jede na svém sportovním kole rychlostí 50 mph a ve druhé polovině jízdy 70 mph z domova na pláž. Jaká bude jeho průměrná rychlost?

Řešení:

Pro výpočet použijte následující údaje.

V tomto příkladu Rey šel na cestu s určitou rychlostí a zde by průměr vycházel ze vzdálenosti.

Výpočet lze provést následujícím způsobem,

Zde můžeme vypočítat harmonický průměr pro průměrnou rychlost sportovního kola Rey.

Harmonický průměr = n / ∑ [1 / X _i ]

• = 2 / (1/50 + 1/70)
• = 2 / 0,03

Průměrná rychlost sportovního kola Rey je 58,33.

Použití a relevance

Harmonické prostředky, stejně jako jiné průměrné vzorce, mají také několik použití a používají se hlavně v oblasti financí k průměrování určitých údajů, jako jsou cenové násobky. Finanční násobky, jako je poměr P / E, nesmí být zprůměrovány pomocí běžného průměru nebo aritmetického průměru, protože tyto střední hodnoty jsou vychýleny směrem k vyšším hodnotám. Harmonické prostředky lze dále použít také k identifikaci určitého typu vzorů, jako jsou Fibonacciho sekvence, které se používají hlavně v technické analýze tržními techniky.

Harmonický průměr se také zabývá průměrem jednotek, jako jsou rychlosti, poměry nebo rychlost atd. Je také důležité si uvědomit, že je ovlivněn extrémními hodnotami v daném souboru dat nebo v dané sadě pozorování.

Harmonický průměr je definován přísně a je založen na všech hodnotách nebo všech pozorováních v daném souboru dat nebo vzorku a může být vhodný pro další matematické zpracování. Stejně jako geometrický průměr, ani harmonický průměr není příliš ovlivněn fluktuacemi pozorování nebo odběru vzorků. To by přisuzovalo větší význam malým hodnotám nebo malým pozorováním a bude to užitečné pouze tehdy, když těmto malým hodnotám nebo malým pozorováním bude třeba věnovat větší váhu.