Čas zdvojnásobení (význam, vzorec) | Krok za krokem výpočet
Co je čas na zdvojnásobení?
Zdvojnásobení času se vztahuje k časovému období požadovanému ke zdvojnásobení hodnoty nebo velikosti investice, populace, inflace atd. A vypočítá se vydělením log 2 součinem počtu složení za rok a přirozeným logem jedna plus míra pravidelný návrat.
Vzorec pro zdvojnásobení času
Matematicky je vzorec pro zdvojnásobení času reprezentován jako,
Čas zdvojnásobení = ln 2 / [n * ln (1 + r / n)]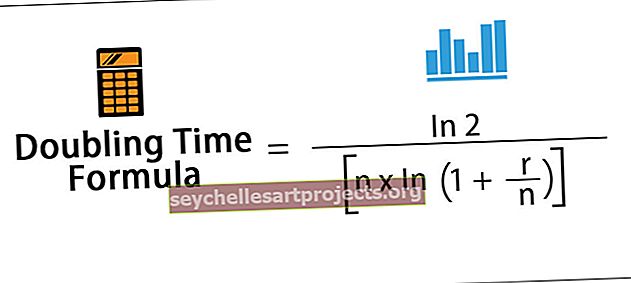
kde
- r = míra ročního výnosu
- n = ne. období slučování za rok
V případě kontinuálního složeného vzorce je výpočet doby zdvojnásobení vyjádřený v letech odvozen vydělením přirozeného logaritmu 2 mírou ročního výnosu (od (1 + r / n) ~ er / n).
Čas zdvojnásobení = ln 2 / [n * ln er / n]
- = ln 2 / [n * r / n]
- = ln 2 / r
kde r = míra návratnosti
Výše uvedený vzorec lze dále rozšířit jako,
Čas zdvojnásobení = 0,69 / r = 69 / r%, což je známé jako pravidlo 69.
Výše uvedený vzorec je však také upraven jako pravidlo 72, protože se nepoužívá prakticky spojité složení, a proto 72 dává realističtější hodnotu časového období pro méně časté intervaly složení. Na druhou stranu je v módě také pravidlo 70, které se používá pouze pro snadný výpočet.
Výpočet zdvojnásobení času (krok za krokem)
- Krok 1: Nejprve určete míru roční návratnosti dané investice. Roční úroková sazba je označena písmenem „r“.
- Krok 2: Dále zkuste zjistit frekvenci skládání za rok, která může být 1, 2, 4 atd., Což odpovídá ročnímu složení, pololetně a čtvrtletně. Počet slučovacích období za rok je označen písmenem „n“. (Tento krok není vyžadován pro průběžné skládání)
- Krok 3: Dále se vypočítá míra periodického výnosu vydělením míry ročního výnosu počtem složených období za rok. Míra pravidelného výnosu = r / n
- Krok 4: Nakonec v případě diskrétního složení se vzorec v letech vypočítá vydělením přirozeného logaritmu čísla 2 součinem č. složeného období za rok a přirozený logaritmus jedné plus míra periodického návratu jako čas zdvojnásobení = ln 2 / [n * ln (1 + r / n)]
Na druhou stranu, v případě kontinuálního skládání je vzorec vyjádřený v letech odvozen vydělením přirozeného logaritmu 2 mírou ročního výnosu jako,
Čas zdvojnásobení = ln 2 / r
Příklad
Tuto šablonu Excel vzorce zdvojnásobení času si můžete stáhnout zde - šablonu Excel vzorce zdvojnásobení času
Vezměme si příklad, kde je roční výnos 10%. Vypočítejte dobu zdvojnásobení pro následující slučovací období:
- Denně
- Měsíční
- Čtvrtletní
- Pololetní
- Roční
- Kontinuální
Vzhledem k tomu, míra ročního výnosu, r = 10%
# 1 - denní složení
Od denního složení tedy n = 365
Čas zdvojnásobení = ln 2 / [n * ln (1 + r / n)]
- = ln 2 / [365 * ln (1 + 10% / 365)
- = 6,9324 let
# 2 - Měsíční složení
Od měsíčního složení tedy n = 12
Čas zdvojnásobení = ln 2 / [n * ln (1 + r / n)]
- = ln 2 / [12 * ln (1 + 10% / 12)
- = 6 9603 let
# 3 - Čtvrtletní složení
Od čtvrtletního složení tedy n = 4
Čas zdvojnásobení = ln 2 / [n * ln (1 + r / n)]
- = ln 2 / [4 * ln (1 + 10% / 4)
- = 7,0178 let
# 4 - Pololetní složení
Od pololetního složení tedy n = 2
Čas zdvojnásobení = ln 2 / [n * ln (1 + r / n)]
- = ln 2 / [2 * ln (1 + 10% / 2)
- = 7,1033 let
# 5 - Roční složení
Od ročního složení, tedy n = 1,
Čas zdvojnásobení = ln 2 / [n * ln (1 + r / n)]
- = ln 2 / [1 * ln (1 + 10% / 1)
- = 7,2725 let
# 6 - Kontinuální skládání
Od kontinuálního složení
Čas zdvojnásobení = ln 2 / r
- = ln 2/10%
- = 6,9315 let
Proto bude výpočet pro různá slučovací období -

Výše uvedený příklad ukazuje, že doba zdvojnásobení závisí nejen na míře ročního výnosu investice, ale také na č. kombinovaných období za rok a zvyšuje se s nárůstem frekvence skládání za rok.
Relevance a použití
Je důležité, aby investiční analytik rozuměl konceptu zdvojnásobení času, protože jim pomáhá zhruba odhadnout, za kolik let bude trvat, než se investice zdvojnásobí. Na druhou stranu investoři používají tuto metriku k vyhodnocení různých investic nebo tempa růstu portfolia odchodu do důchodu. Ve skutečnosti nachází uplatnění v odhadu, jak dlouho by zemi trvalo zdvojnásobení jejího reálného hrubého domácího produktu (HDP).