Z Testovací vzorec ve statistice | Výpočet krok za krokem (příklady)

Vzorec pro výpočet Z testu ve statistice

Z Test ve statistice odkazuje na test hypotézy, který se používá k určení, zda se vypočtené dva průměry vzorků liší, v případě, že jsou k dispozici standardní odchylky a vzorek je velký.

Z = (x - μ) / ơ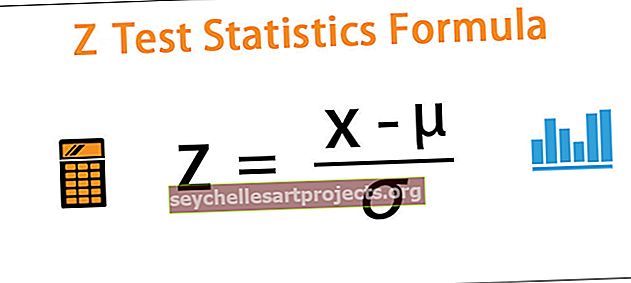

kde x = libovolná hodnota z populace

μ = průměr populace
ơ = směrodatná odchylka populace

V případě vzorku se vzorec pro statistiku hodnoty z-testu vypočítá odečtením střední hodnoty vzorku od hodnoty x a poté se výsledek vydělí standardní směrodatnou odchylkou. Matematicky je reprezentován jako,

Z = (x - x_mean ) / s

kde

x = libovolná hodnota ze vzorku
x_mean = průměr vzorku
s = směrodatná odchylka vzorku

Výpočet testu Z (krok za krokem)

Vzorec pro statistiku z-testu pro populaci je odvozen pomocí následujících kroků:

Krok 1: Nejprve vypočítejte průměrné hodnoty populace a směrodatnou odchylku populace na základě pozorování zachyceného v průměrné hodnotě populace a každé pozorování je označeno x _i . Celkový počet pozorování v populaci je označen N.

Průměr populace

Standardní odchylka populace,

Krok 2: Nakonec se statistika z-testu vypočítá odečtením průměrné hodnoty populace z proměnné a poté se výsledek vydělí standardní směrodatnou odchylkou populace, jak je uvedeno níže.

Z = (x - μ) / ơ

Vzorec pro statistiku z-testu pro vzorek je odvozen pomocí následujících kroků:

Krok 1: Nejprve vypočítejte průměr vzorku a směrodatnou odchylku vzorku stejně jako výše. Zde je celkový počet pozorování ve vzorku označen n takovým, že n <N.

Průměrný vzorek,

Standardní směrodatná odchylka,

Krok 2: Nakonec se statistika z-testu vypočítá odečtením střední hodnoty vzorku od hodnoty x a poté se výsledek vydělí standardní směrodatnou odchylkou vzorku, jak je znázorněno níže.

Z = (x - x_mean ) / s

Příklady

Tuto šablonu Z Test Formula Formula Excel si můžete stáhnout zde - Šablona Z Test Formula Formula

Příklad č. 1

Předpokládejme populaci studentů ve škole, kteří se zúčastnili třídního testu. Průměrné skóre v testu je 75 a směrodatná odchylka je 15. Určete skóre z-testu Davida, který v testu zaznamenal 90 bodů.

Vzhledem k tomu,

Průměr populace, μ = 75
Standardní odchylka populace, ơ = 15

Proto lze statistiku z-testu vypočítat jako,

Z = (90 - 75) / 15

Statistika testu Z bude -

Z = 1

Proto je Davidovo skóre testu o jednu směrodatnou odchylku nad průměrným skóre populace, tj. Podle tabulky z-skóre, o 84,13% studentů méně skóre než David.

Příklad č. 2

Vezměme si příklad 30 studentů, kteří byli vybráni jako součást výběrového týmu, který měl být dotazován, abychom zjistili, kolik tužek bylo za týden použito. Určete skóre z-testu pro 3. studenta na základě daných odpovědí: 3, 2, 5, 6, 4, 7, 4, 3, 3, 8, 3, 1, 3, 6, 5, 2, 4 , 3, 6, 4, 5, 2, 2, 4, 4, 2, 8, 3, 6, 7.

Vzhledem k tomu,

x = 5, od odpovědi 3. studenta, je 5
Velikost vzorku, n = 30

Průměr vzorku, = (3 + 2 + 5 + 6 + 4 + 7 + 4 + 3 + 3 + 8 + 3 + 1 + 3 + 6 + 5 + 2 + 4 + 3 + 6 + 4 + 5 + 2 + 2 + 4 + 4 + 2 + 8 + 3 + 6 + 7) / 30

Průměr = 4,17

Nyní lze standardní směrodatnou odchylku vypočítat pomocí výše uvedeného vzorce.

ơ = 1,90

Proto lze skóre z-testu pro 3. studenta vypočítat jako,

Z = (x - x) / s

Z = (5–17) / 1,90
Z = 0,44

Využití 3. studenta je tedy 0,44násobek standardní odchylky nad průměrným využitím vzorku, tj. Podle tabulky z-score používá 67% studentů méně tužek než 3. student.

Příklad č. 3

Níže jsou uvedena data pro výpočet statistik Z testu

Podrobný výpočet statistik Z testu naleznete v níže uvedeném listu aplikace Excel.

Relevance a použití

Je velmi důležité porozumět pojmu statistika z-testu, protože se obvykle používá vždy, když je diskutabilní, zda statistika testu sleduje normální rozdělení podle příslušné nulové hypotézy. Je však třeba mít na paměti, že z-test se používá pouze v případě, že je velikost vzorku větší než 30, jinak se použije t-test.

seychellesartprojects.org