seychellesartprojects.org

Vzorec pro určení velikosti vzorku populace

Vzorec velikosti vzorku pomáhá při výpočtu nebo určení minimální velikosti vzorku, která je požadována, aby bylo možné znát adekvátní nebo správný podíl populace spolu s úrovní spolehlivosti a mírou chyby.

Pojem „vzorek“ označuje část populace, která nám umožňuje vyvodit závěry o populaci, a proto je důležité, aby velikost vzorku byla dostatečně adekvátní, aby bylo možné učinit smysluplné závěry. Jinými slovy, je to minimální velikost, která je potřebná k odhadu skutečného podílu populace s požadovanou mírou chyb a úrovně spolehlivosti. Stanovení vhodné velikosti vzorku je tedy jedním z opakujících se problémů statistické analýzy. Jeho rovnici lze odvodit pomocí velikosti populace, kritické hodnoty normálního rozdělení, podílu vzorku a míry chyby.

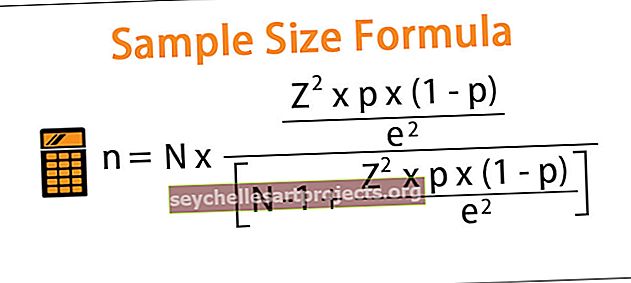
kde,

• N = velikost populace,
• Z = kritická hodnota normálního rozdělení na požadované úrovni spolehlivosti,
• p = podíl vzorku,
• e = mez chyby

Jak vypočítat velikost vzorku? (Krok za krokem)

• Krok 1: Nejprve určete velikost populace, což je celkový počet odlišných entit ve vaší populaci a je označena N. [Poznámka: V případě, že velikost populace je velmi velká, ale přesný počet není znám, použijte 100 000 protože velikost vzorku se u populací větších než toto příliš nemění.]
• Krok 2: Dále určete kritickou hodnotu normálního rozdělení na požadované úrovni spolehlivosti. Například kritická hodnota při 95% úrovni spolehlivosti je 1,96.
• Krok 3: Dále určete podíl vzorku, který lze použít z výsledků předchozího průzkumu nebo který lze shromáždit spuštěním malého pilotního průzkumu. [Poznámka: pokud si nejste jisti, můžete vždy použít 0,5 jako konzervativní přístup a poskytne největší možnou velikost vzorku.]
• Krok 4: Dále určete hranici chyby, což je rozsah, ve kterém se očekává, že skutečná populace bude ležet . [Poznámka: Čím menší je míra chyby, tím větší je přesnost, a tedy přesná odpověď.]
• Krok 5: Nakonec lze rovnici velikosti vzorku odvodit pomocí velikosti populace (krok 1), kritické hodnoty normálního rozdělení na požadované úrovni spolehlivosti (krok 2), podílu vzorku (krok 3) a míry chyby (krok 4) jak je uvedeno níže.

Příklady

Tuto šablonu vzorce pro vzorovou velikost Excel si můžete stáhnout zde - Šablona vzorce pro velikost vzorku Excel

Příklad č. 1

Vezměme si příklad maloobchodníka, který má zájem zjistit, kolik zákazníků si od něho koupilo položku poté, co si v určitý den prohlédlo jejich web. Vzhledem k tomu, že jejich webové stránky mají v průměru 10 000 zhlédnutí za den, určete velikost vzorku zákazníků, které mají sledovat, na 95% úrovni spolehlivosti s 5% mírou chyb, pokud:

• Nejsou si jisti aktuálním konverzním poměrem.
• Z předchozích průzkumů vědí, že míra konverze je 5%.

Vzhledem k tomu,

• Velikost populace, N = 10 000
• Kritická hodnota na 95% úrovni spolehlivosti, Z = 1,96
•  Mez chyby, e = 5% nebo 0,05

1 - Jelikož aktuální přepočítací koeficient není znám, předpokládejme p = 0,5

Proto lze velikost vzorku vypočítat pomocí vzorce jako,

= (10 000 * (1,96 2) * 0,5 * (1-0,5) / (0,05 2) / (10 000 - 1 + ((1,96 2) * 0,5 * (1-0,5) / (0,05 2))))

Pro odvození smysluplného závěru tedy bude stačit 370 zákazníků.

2 - Aktuální přepočítací koeficient je p = 5% nebo 0,05

Proto lze velikost vzorku vypočítat pomocí výše uvedeného vzorce jako,

= (10 000 * (1,96 2) * 0,05 * (1-0,05) / (0,05 2) / (10 000 - 1 + ((1,96 2) * 0,05 * (1-0,05) / (0,05 2))))

Proto bude v tomto případě pro odvození smysluplného závěru dostatečná velikost 72 zákazníků.

Příklad č. 2

Vezměme si výše uvedený příklad a v tomto případě předpokládejme, že velikost populace, tj. Denní zobrazení webu, je mezi 100 000 a 120 000, ale přesná hodnota pak není známa. Zbytek hodnot je stejný spolu s konverzním poměrem 5%. Vypočítejte velikost vzorku pro 100 000 i 120 000.

Vzhledem k tomu,

• Podíl vzorku, p = 0,05
• Kritická hodnota na 95% úrovni spolehlivosti, Z = 1,96
•  Mez chyby, e = 0,05

Proto lze velikost vzorku pro N = 100 000 vypočítat jako,

= (100000 * (1,96 2) * 0,05 * (1-0,05) / (0,05 2) / (100000 - 1 + ((1,96 2) * 0,05 * (1-0,05) / (0,05 2))))

Proto lze velikost vzorku pro N = 120 000 vypočítat jako,

= (120000 * (1,96 2) * 0,05 * (1-0,05) / (0,05 2) / (120000 - 1 + ((1,96 2) * 0,05 * (1-0,05) / (0,05 2))))

Proto je dokázáno, že jak se velikost populace zvětšuje na velmi velkou, stává se při výpočtu velikosti vzorku irelevantní.

Relevance a použití

Výpočet velikosti vzorku je důležitý pro pochopení konceptu vhodné velikosti vzorku, protože se používá pro validitu výsledků výzkumu. V případě, že je příliš malý, nepřinese platné výsledky, zatímco příliš velký vzorek může být ztrátou peněz i času. Statisticky se významná velikost vzorku používá převážně pro průzkumy trhu, zdravotnictví a vzdělávání.