Vzorec odchylky portfolia (příklad) | Jak vypočítat odchylku portfolia?
Co je to varianta portfolia?
Pojem „rozptyl portfolia“ označuje statistickou hodnotu moderní investiční teorie, která pomáhá při měření rozptylu průměrných výnosů portfolia od jeho průměru. Stručně řečeno, určuje celkové riziko portfolia. Lze jej odvodit na základě váženého průměru individuální rozptylu a vzájemné kovariance.
Vzorec odchylky portfolia
Matematicky je vzorec rozptylu portfolia skládající se ze dvou aktiv reprezentován jako,
Vzorec odchylky portfolia = w 1 2 * ơ 1 2 + w 2 2 * ơ 2 2 + 2 * ρ 1,2 * w 1 * w 2 * ơ 1 * ơ 2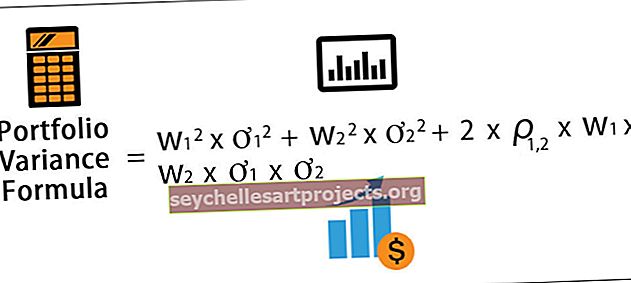
kde,
- w i = váha portfolia aktiva i
- ơ i 2 = individuální rozptyl aktiva i
- ρ i, j = korelace mezi aktivem i a aktivem j
Opět lze rozptyl dále rozšířit na portfolio více ne. aktiv, například portfolio 3 aktiv lze představovat jako,
Vzorec pro rozptyl portfolia = w 1 2 * ơ 1 2 + w 2 2 * ơ 2 2 + w 3 2 * ơ 3 2 + 2 * ρ 1,2 * w 1 * w 2 * ơ 1 * ơ 2 + 2 * ρ 2,3 * w 2 * w 3 * ơ 2 * ơ 3 + 2 * ρ 3,1 * w 3 * w 1 * ơ 3* ơ 1
Vysvětlení vzorce odchylky portfolia
Vzorec odchylky portfolia konkrétního portfolia lze odvodit pomocí následujících kroků:
Krok 1: Nejprve určete váhu každého aktiva v celkovém portfoliu a vypočítá se vydělením hodnoty aktiva celkovou hodnotou portfolia. Váha i-tého aktiva je označena w i .
Krok 2: Dále určete směrodatnou odchylku každého aktiva a vypočítá se na základě průměrné a skutečné návratnosti každého aktiva. Směrodatná odchylka i-tého aktiva je označena ơ i . Druhá mocnina směrodatné odchylky je rozptyl, tj. Ơ i 2.
Krok 3: Dále určete korelaci mezi aktivy a v podstatě zachycuje pohyb každého aktiva ve srovnání s jiným aktivem. Korelace je označena ρ.
Krok 4: Nakonec je vzorec portfoliového rozptylu dvou aktiv odvozen na základě váženého průměru individuálního rozptylu a vzájemného kovariance, jak je uvedeno níže.
Vzorec odchylky portfolia = w 1 * ơ 1 2 + w 2 * ơ 2 2 + 2 * ρ 1,2 * w 1 * w 2 * ơ 1 * ơ 2
Příklad vzorce odchylky portfolia (s šablonou Excel)
Tuto šablonu Excel Portfolio Variance Formula si můžete stáhnout zde - Šablona Excel Portfolio Variance Formula
Vezměme si příklad portfolia, které se skládá ze dvou akcií. Hodnota akcie A je 60 000 $ a její standardní odchylka je 15%, zatímco hodnota akcie B je 90 000 $ a její standardní odchylka je 10%. Mezi oběma akciemi existuje korelace 0,85. Určete rozptyl.
Vzhledem k tomu,
- Směrodatná odchylka zásoby A, ơ A = 15%
- Směrodatná odchylka zásoby B, ơ B = 10%
Korelace, ρ A, B = 0,85
Níže jsou uvedeny údaje pro výpočet rozptylu portfolia dvou akcií.

Hmotnost akcií A, w A = 60 000 $ / (60 000 $ + 90 000 $) * 100%

Hmotnost skladu A = 40% nebo 0,40
Hmotnost akcií B, w B = 90 000 $ / (60 000 $ + 90 000 $) * 100%

Hmotnost akcií B = 60% nebo 0,60
Proto bude výpočet rozptylu portfolia následující,

Rozptyl = w A 2 * ơ A 2 + w B 2 * ơ B 2 + 2 * ρ A, B * w A * w B * ơ A * ơ B
= 0,4 ^ 2 * (0,15) 2 + 0,6 ^ 2 * (0,10) 2 + 2 * 0,85 * 0,4 * 0,6 * 0,15 * 0,10

Proto je rozptyl 1,33%.
Relevance a použití
Jednou z nejpozoruhodnějších vlastností portfolia var je skutečnost, že jeho hodnota je odvozena na základě váženého průměru jednotlivých odchylek každého z aktiv upraveného podle jejich měřítek. To naznačuje, že celková odchylka je menší než prostý vážený průměr jednotlivých odchylek každé akcie v portfoliu. Je třeba poznamenat, že portfolio s cennými papíry, které mají mezi sebou nižší korelaci, končí s nižší variabilitou portfolia.
Pochopení vzorce rozptylu portfolia je také důležité, protože nachází uplatnění v teorii moderního portfolia, která je postavena na základním předpokladu, že normální investoři mají v úmyslu maximalizovat své výnosy při minimalizaci rizika, jako je rozptyl. Investor obvykle sleduje takzvanou efektivní hranici a jedná se o nejnižší úroveň rizika nebo volatility, při které může investor dosáhnout svého cílového výnosu. Nejčastěji by investoři investovali do nekorelovaných aktiv, aby snížili riziko podle moderní teorie portfolia.
Existují případy, kdy aktiva, která mohou být jednotlivě riziková, mohou nakonec snížit rozptyl portfolia, protože taková investice pravděpodobně poroste, když ostatní investice poklesnou. Tato snížená korelace jako taková může pomoci snížit rozptyl hypotetického portfolia. Úroveň rizika portfolia se obvykle měří pomocí standardní odchylky, která se počítá jako druhá odmocnina rozptylu. Očekává se, že rozptyl zůstane vysoký, i když jsou datové body daleko od průměru, což nakonec povede také k vyšší celkové úrovni rizika v portfoliu.