seychellesartprojects.org

Definice metody regrese nejmenších čtverců

Metoda regrese metodou nejmenších čtverců je formou regresní analýzy, která stanoví vztah mezi závislou a nezávislou proměnnou spolu s lineární přímkou. Tato řada se označuje jako „řada nejvhodnější“.

Regresní analýza je statistická metoda, pomocí které lze odhadnout nebo předpovědět neznámé hodnoty jedné proměnné ze známých hodnot jiné proměnné. Proměnná, která se používá k predikci zájmu proměnné, se nazývá nezávislá nebo vysvětlující proměnná a proměnná, která se předpovídá, se nazývá závislá nebo vysvětlená proměnná.

Uvažujme dvě proměnné x & y. Ty jsou vyneseny do grafu s hodnotami x na hodnotách osy x y na ose y. Tyto hodnoty jsou znázorněny tečkami v níže uvedeném grafu. Mezi tečkami je nakreslena přímka - označovaná jako nejvhodnější čára.

Cílem regrese nejmenších čtverců je zajistit, aby čára vedená sadou poskytnutých hodnot vytvořila nejbližší vztah mezi hodnotami.

Regresní vzorec nejmenších čtverců

Regresní čára v metodě nejmenších čtverců se vypočítá podle následujícího vzorce -

ŷ = a + bx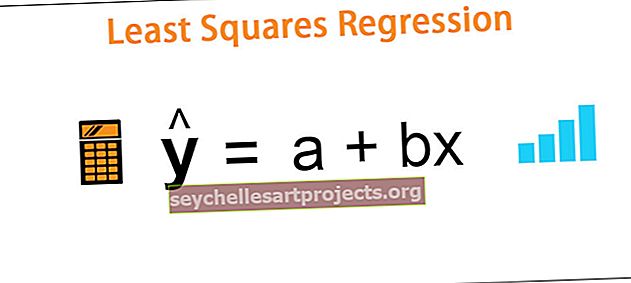

Kde,

• ŷ = závislá proměnná
• x = nezávislá proměnná
• a = průsečík y
• b = sklon přímky

Sklon přímky b se vypočítá podle následujícího vzorce -

Nebo

X-intercept, 'a' se počítá podle následujícího vzorce -

Line of Best Fit in the Least Square Regression

Nejvhodnější čára je přímka nakreslená rozptylem datových bodů, který nejlépe představuje vztah mezi nimi.

Uvažujme následující graf, kde je množina dat vynesena podél osy xay. Tyto datové body jsou reprezentovány pomocí modrých teček. Těmito body jsou nakresleny tři čáry - zelená, červená a modrá čára. Zelená čára prochází jedním bodem a červená čára prochází třemi datovými body. Modrá čára však prochází čtyřmi datovými body a vzdálenost mezi zbývajícími body k modré čáře je ve srovnání s ostatními dvěma čarami minimální.

Ve výše uvedeném grafu představuje modrá čára nejvhodnější přímku, protože leží nejblíže ke všem hodnotám a vzdálenost mezi body mimo přímku k přímce je minimální (tj. Vzdálenost mezi zbytky k přímce nejvhodnější - označované také jako součet čtverců zbytků). V dalších dvou řádcích, oranžové a zelené, je vzdálenost mezi zbytky řádků větší ve srovnání s modrou čarou.

Metoda nejmenších čtverců poskytuje nejužší vztah mezi závislými a nezávislými proměnnými tím, že minimalizuje vzdálenost mezi rezidui a řádkou nejlepšího přizpůsobení, tj. Součet čtverců reziduí je při tomto přístupu minimální. Proto termín „nejmenší čtverce“.

Příklady linie nejmenších čtverců

Použijme tyto vzorce v níže uvedené otázce -

Tuto šablonu aplikace Regrese nejmenších čtverců si můžete stáhnout zde - Šablona aplikace Regrese nejmenších čtverců Excel

Příklad č. 1

Podrobnosti týkající se zkušeností techniků ve společnosti (za několik let) a jejich hodnocení výkonu jsou uvedeny v následující tabulce. Pomocí těchto hodnot odhadněte hodnocení výkonu pro technika s 20 lety zkušeností.

Řešení -

Pro výpočet nejmenších čtverců nejprve vypočítáme průsečík Y (a) a sklon přímky (b) následujícím způsobem -

Sklon přímky (b)

• b = 6727 - [(80 * 648) / 8] / 1018 - [(80) 2/8]
• = 247/218
• = 1,13

Y-průsečík (a)

• a = 648 - (1,13) (80) / 8
• = 69,7

Regresní čára se vypočítá následovně -

Dosazením 20 za hodnotu x ve vzorci,

• ŷ = a + bx
• ŷ = 69,7 + (1,13) (20)
• ŷ = 92,3

Hodnocení výkonu pro technika s 20 lety zkušeností se odhaduje na 92,3.

Příklad č. 2

Regrese rovnice nejmenších čtverců pomocí aplikace Excel

Regresní rovnici nejmenších čtverců lze vypočítat pomocí aplikace Excel podle následujících kroků -

• Vložte tabulku dat do aplikace Excel.

• Vložte bodový graf pomocí datových bodů.

• Vložte trendovou čáru do rozptylového grafu.

• V části Možnosti trendové čáry - vyberte lineární trendovou čáru a vyberte rovnici zobrazení v grafu.

• Regresní rovnice nejmenších čtverců pro danou sadu dat aplikace Excel je zobrazena v grafu.

Vypočítá se tedy regresní rovnice nejmenších čtverců pro danou sadu dat aplikace Excel. Pomocí rovnice lze provádět predikce a analýzy trendů. Nástroje aplikace Excel také poskytují podrobné regresní výpočty.

Výhody

• Metoda nejmenších čtverců regresní analýzy je nejvhodnější pro predikční modely a analýzu trendů. Nejlépe se používá v oblastech ekonomiky, financí a akciových trhů, kde je hodnota jakékoli budoucí proměnné předpovídána pomocí existujících proměnných a vztahu mezi nimi.
• Metoda nejmenších čtverců poskytuje nejužší vztah mezi proměnnými. Rozdíl mezi součty čtverců zbytků k řádce nejvhodnější je u této metody minimální.
• Výpočetní mechanismus je jednoduchý a snadno použitelný.

Nevýhody

• Metoda nejmenších čtverců se opírá o stanovení nejužšího vztahu mezi danou sadou proměnných. Výpočetní mechanismus je citlivý na data a v případě jakýchkoli odlehlých hodnot (výjimečných dat) mohou mít výsledky zásadní vliv.
• Tento typ výpočtu je nejvhodnější pro lineární modely. Pro nelineární rovnice se používají důkladnější výpočetní mechanismy.

Závěr

Metoda nejmenších čtverců je jednou z nejoblíbenějších metod pro predikční modely a analýzu trendů. Při správném výpočtu poskytuje nejlepší výsledky.