seychellesartprojects.org

Vzorec pro výpočet průměru

Průměr je hodnota, která se používá k vyjádření množiny hodnot dat, stejně jako průměr vypočtený z celých dat, a tento vzorec se vypočítá sečtením všech hodnot dané množiny, označených součtem X a vydělením počtem hodnoty uvedené v množině označené N.

Průměr = (a ₁ + a ₂ +…. + A _n ) / n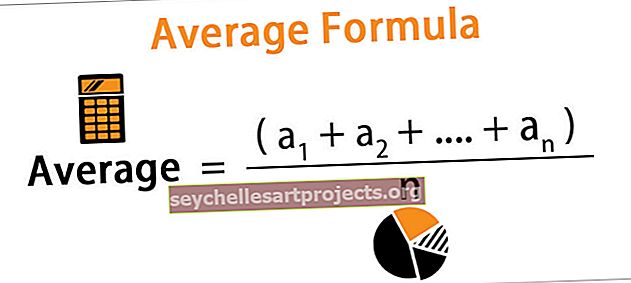

• kde _i = _i -té pozorování
• n = počet pozorování

Vysvětlení

Výpočet průměru lze vypočítat pomocí následujících kroků:

• Krok 1: Nejprve určete pozorování a jsou označeny ₁ , ₂ , ... .., _n odpovídající 1. pozorování, 2. pozorování, ..., n. Pozorování.
• Krok 2: Dále určete počet pozorování a je označen n.
• Krok 3: Nakonec se průměr vypočítá sečtením všech pozorování a následným vydělením výsledku počtem pozorování, jak je uvedeno níže.

Průměr = (a ₁ + a ₂ +…. + A _n ) / n

Příklady

Tuto šablonu Excel s průměrným vzorcem si můžete stáhnout zde - Šablona Excel s průměrným vzorcem

Příklad č. 1

Vezměme si příklad Johna, který se zapsal na magisterský program pro vědu o životním prostředí. Tříletý studijní program je rozdělen do šesti semestrů a konečné průměrné procento se vypočítá na základě procentních hodnot zaznamenaných ve všech semestrech. Vypočítejte Johnovo konečné procento na základě jeho následujícího skóre:

Níže jsou uvedeny údaje pro výpočet průměrného procenta.

Vzhledem k tomu,

a ₁ = 79%, a ₂ = 81%, a ₃ = 74%, a ₄ = 70%, a ₅ = 82%, a ₆ = 85%, n = 6

S využitím výše uvedených informací bude výpočet průměru následující,

•   Průměr = (79% + 81% + 74% + 70% + 82% + 85%) / 6

Průměr bude -

• Průměr = 78,50%

Proto David získal v programu promoce konečné procento 78,5%.

Použití

Jak název „průměr“ napovídá, odkazuje na ústřední bod mezi množinou pozorování, a pokud je používán v oblasti matematiky, představuje číslo, které obvykle znamená skupinu čísel. Termín se často používá k vyjádření čísla, které představuje skupinu lidí nebo věcí. Je to velmi důležité, protože pomáhá shrnout velké množství dat do jediné hodnoty a také naznačuje, že kolem jedné hodnoty existuje určitá nekonzistence v původních datech, která tvoří velmi důležitou součást teorie centrální tendence.