seychellesartprojects.org

Co je R Squared (R2) v regrese?

R-kvadrát (R2) je důležité statistické měřítko, kterým je regresní model, který představuje podíl rozdílu nebo rozptylu ve statistickém vyjádření pro závislou proměnnou, což lze vysvětlit nezávislou proměnnou nebo proměnnými. Stručně řečeno, určuje, jak dobře budou data odpovídat regresnímu modelu.

R na druhou vzorec

Pro výpočet R na druhou musíte určit korelační koeficient a poté musíte výsledek umocnit.

R na druhou vzorec = r2

Kde r lze korelační koeficient vypočítat níže:

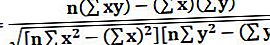
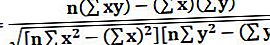
Kde,

• r = Korelační koeficient
• n = číslo v dané datové sadě
• x = první proměnná v kontextu
• y = druhá proměnná

Vysvětlení

Pokud existuje nějaký vztah nebo korelace, která může být lineární nebo nelineární mezi těmito dvěma proměnnými, pak to indikuje, zda dojde ke změně nezávislé proměnné v hodnotě, pak se druhá závislá proměnná pravděpodobně změní v hodnotě, řekněme lineárně nebo ne- lineárně.

Čitatelská část vzorce provádí test, zda se pohybují společně, a odstraňuje jejich jednotlivé pohyby a relativní sílu obou pohybujících se společně a jmenovatelská část vzorce mění měřítko čitatele tak, že získá druhou odmocninu součinu rozdílů proměnné z jejich čtvercových proměnných. A když načtete tento výsledek na druhou, dostaneme R na druhou, což není nic jiného než koeficient determinace.

Příklady

Tuto šablonu R Squared Formula Excel si můžete stáhnout zde - Šablona R Squared Formula Excel

Příklad č. 1

Zvažte následující dvě proměnné x a y, je nutné vypočítat R na druhou v regrese.

Řešení:

Pomocí výše uvedeného vzorce musíme nejprve vypočítat korelační koeficient.

Máme všechny hodnoty ve výše uvedené tabulce s n = 4.

Pojďme nyní zadat hodnoty do vzorce, abychom dospěli k obrázku.

r = (4 * 26 046,25) - (265,18 * 326,89) / √ [(4 * 21 274,94) - (326,89) 2] * [(4 * 31 901,89) - (326,89) 2]

r = 17 501,06 / 17 512,88

Korelační koeficient bude-

r = 0,99932480

Výpočet bude tedy následující,

r2 = (0,99932480) 2

R na druhou vzorec v regresi

r2 = 0,998650052

Příklad č. 2

Indie jako rozvojová země chce provést nezávislou analýzu, zda změny cen ropy ovlivnily její rupie. Následuje historie cen ropy Brent a ocenění rupií vůči dolary, které v těchto letech v průměru převládaly níže.

RBI, indická centrální banka vás oslovila, abyste na příštím setkání poskytli stejnou prezentaci. Zjistěte, zda pohyby ropy ovlivňují pohyby rupií za dolar?

Řešení:

Pomocí výše uvedeného vzorce pro korelaci můžeme nejprve vypočítat korelační koeficient. Považujeme průměrnou cenu ropy za jednu proměnnou, řekněme x, a za rupii za dolar považujeme za jinou proměnnou jako y.

Máme všechny hodnoty ve výše uvedené tabulce s n = 6.

Pojďme nyní zadat hodnoty do vzorce, abychom dospěli k obrázku.

r = (6 * 23592,83) - (356,70 * 398,59) / √ [(6 * 22829,36) - (356,70) 2] * [(6 * 26529,38) - (398,59) 2]

r = -620,06 / 1715,95

Korelační koeficient bude-

r = -0,3614

Výpočet bude tedy následující,

r2 = (-0,3614) 2

R na druhou vzorec v regresi

r2 = 0,1306

Analýza: Ukazuje se, že existuje malý vztah mezi změnami cen ropy a změnami cen indické rupie. Se zvyšováním cen ropy ovlivňují také změny v indické rupii. Ale protože R na druhou je pouze 13%, pak změny ceny ropy vysvětlují méně o změnách indické rupie a indická rupie podléhá změnám i v jiných proměnných, které je třeba zohlednit.

Příklad č. 3

Laboratoř XYZ provádí výzkum výšky a hmotnosti a zajímá ji, zda existuje nějaký druh vztahu mezi těmito proměnnými. Po shromáždění vzorku 5000 lidí pro každou kategorii a přišli s průměrnou hmotností a průměrnou výškou v dané skupině.

Níže jsou uvedeny podrobnosti, které shromáždili.

Je třeba vypočítat R na druhou a vyvodit závěr, zda tento model vysvětluje výškové rozdíly ovlivňují odchylky hmotnosti.

Řešení:

Pomocí výše uvedeného vzorce pro korelaci můžeme nejprve vypočítat korelační koeficient. Považujeme výšku za jednu proměnnou, řekněme x a hmotnost považujeme za jinou proměnnou jako y.

Máme všechny hodnoty ve výše uvedené tabulce s n = 6.

Pojďme nyní zadat hodnoty do vzorce, abychom dospěli k obrázku.

r = (7 * 74 058,67) - (1031 * 496,44) / √ [(7 * 153595 - (1031) 2] * [(7 * 35793,59) - (496,44) 2]

r = 6 581,05 / 7 075,77

Korelační koeficient bude-

Korelační koeficient (r) = 0,930

Výpočet bude tedy následující,

r2 = 0,865

Analýza: Korelace je pozitivní a zdá se, že existuje nějaký vztah mezi výškou a hmotností, protože výška zvyšuje váhu osoby, která se také zdá být zvýšena. Zatímco R2 naznačuje, že 86% změn atributů výšky ke změnám hmotnosti a 14% je nevysvětlených.

Relevance a použití

Relevance R na druhou v regresi je její schopnost najít pravděpodobnost budoucích událostí, ke kterým dojde v rámci daných předpovězených výsledků nebo výsledků. Pokud je do modelu přidáno více vzorků, pak by koeficient ukazoval pravděpodobnost nebo pravděpodobnost nového bodu nebo nové datové sady padající na čáru. I když mají obě proměnné silnou souvislost, určení neprokazuje kauzalitu.

Některé z prostorů, kde se R na druhou většinou používá, slouží ke sledování výkonnosti podílových fondů, ke sledování rizika v zajišťovacích fondech, k určení, jak dobře se akcie pohybují s trhem, kde R2 by naznačovalo, kolik pohybů akcií lze vysvětlit pohyby na trhu.