seychellesartprojects.org

Efektivní definice úrokové sazby

Efektivní úroková sazba, známá také jako roční ekvivalentní sazba, je úroková sazba, kterou osoba skutečně zaplatí nebo vydělá na finančním nástroji, která se vypočítá s ohledem na účinek složení za dané časové období.

Efektivní vzorec úrokové sazby

Vzorec efektivní úrokové sazby = (1 + i / n) n -

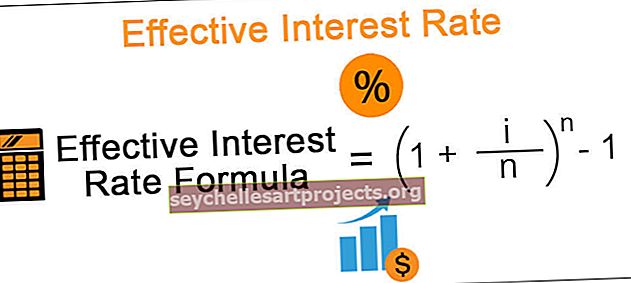
Zde i = roční úroková sazba uvedená v nástroji.

n = Představuje počet slučovacích období za rok.

Výklady

Složením se mění úroková sazba. Proto úroková sazba uvedená na nástroji není pro investora efektivní úrokovou sazbou (roční ekvivalentní sazba). Například pokud je na nástroji napsána úroková sazba 11% a úroková sazba bude kombinována čtyřikrát ročně, pak roční ekvivalentní sazba nemůže být 11%.

Co by to tedy bylo?

Bylo by - (1 + i / n) n - 1 = (1 + 0,11 / 4) 4 - 1 = 1,1123 - 1 = 0,1123 = 11,23%.

To znamená, že 11,23% by byla efektivní úroková sazba pro investora.

I když je změna skromná, není to stejné jako roční úroková sazba uvedená v nástroji.

Příklad

Příklad č. 1

Ting koupil konkrétní nástroj. Úroková sazba uvedená na nástroji je 16%. Investoval kolem 100 000 $. Přístroj se skládá ročně. Jaká by byla efektivní úroková sazba (AER) pro tento konkrétní nástroj? Kolik by každý rok dostal jako úrok?

Efektivní úroková sazba a roční sazba nejsou vždy stejné, protože úroky se každý rok několikrát kombinují. Někdy se úroková sazba zvyšuje pololetně, čtvrtletně nebo měsíčně. A tak se roční ekvivalentní sazba liší od roční úrokové sazby.

Tento příklad vám to ukazuje.

Pojďme vypočítat.

Vzhledem k tomu, že úroková sazba se každoročně zvyšuje, bude zde efektivní vzorec úrokové sazby -

(1 + i / n) n - 1 = (1 + 0,16 / 1) 1 - 1 = 1,16 - 1 = 0,16 = 16%.

To znamená, že v tomto konkrétním příkladu by nebyl žádný rozdíl mezi roční úrokovou sazbou a roční ekvivalentní sazbou (AER).

Každý rok by Ting získal na nástroji úrok = (100 000 $ * 16%) = 16 000 $.

Příklad č. 2

Tong koupil konkrétní nástroj. Úroková sazba uvedená na nástroji je 16%. Investoval kolem 100 000 $. Přístroj se skládá šestkrát ročně. Jaká by byla roční ekvivalentní sazba (AER) pro tento konkrétní nástroj? Kolik by každý rok dostal jako úrok?

Toto je pouze rozšíření předchozího příkladu.

Ale je tu obrovský rozdíl.

V předchozím příkladu byl nástroj sloučen jednou ročně, čímž se roční úroková sazba podobala roční ekvivalentní sazbě.

V tomto případě je však scénář úplně jiný.

Zde máme úrokovou sazbu, která se zvyšuje šestkrát ročně.

Tady je tedy vzorec roční úrokové sazby -

(1 + i / n) n - 1 = (1 + 0,16 / 6) 6 - 1 = 1,171 - 1 = 0,171 = 17,1%.

Nyní můžete vidět, že pokud se úroková sazba zvýší šestkrát ročně, roční ekvivalentní sazba se zcela změní.

Nyní, protože máme efektivní úrokovou sazbu, můžeme vypočítat úrok, který Tong získá na konci roku.

Tong dostane = (100 000 $ * 17,1%) = 17 100 $.

Pokud porovnáme úrok, který Ting získá v předchozím příkladu, s Tongem, protože úroková sazba bude složena odlišně, uvidíme, že v úroku je rozdíl zhruba 1100 USD.

Příklad č. 3

Ping investoval do nástroje. Investovala 10 000 $. Úroková sazba uvedená v nástroji je 18%. Úroky se zvyšují měsíčně. Zjistěte, jak v prvním roce Ping obdrží úrok každý měsíc.

Toto je velmi podrobný příklad roční ekvivalentní sazby.

V tomto příkladu si ukážeme, jak k výpočtu skutečně dochází bez použití vzorce efektivní úrokové sazby.

Pojďme se podívat.

Jelikož se úroková sazba zvyšuje měsíčně, je skutečné rozdělení uvedené úrokové sazby za měsíc = (18/12) = 1,5%.

• V prvním měsíci Ping obdrží úrok ve výši = (10 000 * 1,5%) = 150 USD.
• Ve druhém měsíci Ping obdrží úrok ve výši = {(10 000 + 150) * 1,5%} = (10 150 * 1,5%) = 152,25 USD.
• Ve třetím měsíci Ping obdrží úrok ve výši = {(10 000 + 150 + 152,25) * 1,5%} = (10 302,25 * 1,5%) = 154,53 USD.
• Ve čtvrtém měsíci Ping obdrží úrok ve výši = {(10 000 + 150 + 152,25 + 154,53) * 1,5%} = (10 456,78 * 1,5%) = 156,85 USD.
• V pátém měsíci obdrží Ping úrok = {(10 000 + 150 + 152,25 + 154,53 + 156,85) * 1,5%} = (10 613,63 * 1,5%) = 159,20 USD.
• V šestém měsíci obdrží Ping úrok = {(10 000 + 150 + 152,25 + 154,53 + 156,85 + 159,20) * 1,5%} = (10 772,83 * 1,5%) = 161,59 USD.
• V sedmém měsíci Ping obdrží úrok ve výši = {(10 000 + 150 + 152,25 + 154,53 + 156,85 + 159,20 + 161,59) * 1,5%} = (10 934,42 * 1,5%) = 164,02 USD.
• V osmém měsíci Ping obdrží úrok ve výši = {(10 000 + 150 + 152,25 + 154,53 + 156,85 + 159,20 + 161,59 + 164,02) * 1,5%} = (11098,44 * 1,5%) = 166,48 USD.
• V devátém měsíci Ping obdrží úrok ve výši = {(10 000 + 150 + 152,25 + 154,53 + 156,85 + 159,20 + 161,59 + 164,02 + 166,48) * 1,5%} = (11264,92 * 1,5%) = 168,97 $.
• V desátém měsíci obdrží Ping úrok ve výši = {(10 000 + 150 + 152,25 + 154,53 + 156,85 + 159,20 + 161,59 + 164,02 + 166,48 + 168,97) * 1,5%} = (11433,89 * 1,5%) = 171,51 USD.
• V jedenáctém měsíci Ping obdrží úrok ve výši = {(10 000 + 150 + 152,25 + 154,53 + 156,85 + 159,20 + 161,59 + 164,02 + 166,48 + 168,97 + 171,51) * 1,5%} = (11605,40 * 1,5%) = 174,09 USD.
• Ve dvanáctém měsíci Ping obdrží úrok ve výši = {(10 000 + 150 + 152,25 + 154,53 + 156,85 + 159,20 + 161,59 + 164,02 + 166,48 + 168,97 + 171,51 + 174,09) * 1,5%} = (11779,49 * 1,5%) = 176,69 $.

Celkový úrok, který Ping za rok získal, je -

• (150 + 152,25 + 154,53 + 156,85 + 159,20 + 161,59 + 164,02 + 166,48 + 168,97 + 171,51 + 174,09 + 176,69) = 1956,18 USD.

• Vzorec roční ekvivalentní sazby = (1 + i / n) n - 1 = (1 + 0,18 / 12) 12 - 1 = 1,195618 - 1 = 0,1961818 = 19,5618%.

Takže úrok, který Ping získá, = ($ 10 000 ^ 19,5618%) = $ 1956,18.

Efektivní úroková sazba v aplikaci Excel

Pro nalezení efektivní úrokové sazby nebo roční ekvivalentní sazby v aplikaci Excel používáme funkci Excel EFFECT.

• nominal_rate je úroková sazba
• nper je počet slučovacích období za rok

Podívejme se na příklad níže

• Pokud máte nominální úrokovou sazbu ve výši 10% ročně, pak je roční ekvivalentní sazba stejná jako 10%.
• Pokud máte nominální úrokovou sazbu 10% složenou za šest měsíců, pak je roční ekvivalentní sazba stejná jako 10,25%.
• Pokud máte nominální úrokovou sazbu 10% složenou čtvrtletně, pak je roční ekvivalentní sazba stejná jako 10,38%.
• Pokud máte nominální úrokovou sazbu 10% složenou měsíčně, pak je roční ekvivalentní sazba stejná jako 10,47%.
• Pokud máte nominální úrokovou sazbu 10% složenou denně, pak je efektivní úroková sazba stejná jako 10,52%.

Doporučené četby

Jednalo se o průvodce efektivní úrokovou sazbou a její definicí. Zde diskutujeme vzorec efektivní úrokové sazby spolu s výpočty krok za krokem. Další informace naleznete v následujících článcích

• Příklad záporné úrokové sazby
• Vypočítejte míru účasti
• Rozdíly - diskontní sazba vs úroková sazba
• Vzorec nominální úrokové sazby
• Kointegrace
<