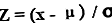seychellesartprojects.org

Vzorec pro výpočet Z-skóre

Z-skóre nezpracovaných dat se týká skóre generovaného měřením toho, kolik standardních odchylek nad nebo pod průměrem populace jsou data, což pomáhá při testování uvažované hypotézy. Jinými slovy, je to vzdálenost datového bodu od střední hodnoty populace, která je vyjádřena jako násobek směrodatné odchylky.

• Z-skóre se mění v rozsahu -3násobku směrodatné odchylky (zcela vlevo od normálního rozdělení) až +3násobku směrodatné odchylky (zcela vpravo od normálního rozdělení).
• Z-skóre mají průměr 0 a směrodatnou odchylku 1.

Rovnice pro z-skóre datového bodu se vypočítá odečtením střední hodnoty populace od datového bodu (označovaného jako x ) a poté se výsledek dělí standardní směrodatnou odchylkou populace. Matematicky je reprezentován jako,

Z skóre = (x - μ) / ơ

kde

• x = Datový bod
• μ = průměr
• ơ = směrodatná odchylka

Výpočet skóre Z (krok za krokem)

Rovnici pro z-skóre datového bodu lze odvodit pomocí následujících kroků:

• Krok 1: Nejprve určete průměr datové sady na základě datových bodů nebo pozorování, které jsou označeny x _i , zatímco celkový počet datových bodů v datové sadě je označen N.

• Krok 2: Dále určete směrodatnou odchylku populace na základě průměrné hodnoty populace μ, datových bodů _xi a počtu datových bodů v populaci N.

• Krok 3: Nakonec se z-skóre odvodí odečtením průměru od datového bodu a poté se výsledek vydělí standardní odchylkou, jak je znázorněno níže.

  

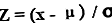
Příklady

Tuto šablonu aplikace Excel Z Score Formula si můžete stáhnout zde - Šablona aplikace Excel Z Score Formula

Příklad č. 1

Vezměme si příklad třídy 50 studentů, kteří minulý týden napsali test z přírodních věd. Dnes je den výsledků a třídní učitel řekl, že John získal v testu 93, zatímco průměrné skóre ve třídě bylo 68. Určete z-skóre pro Johnova testovací známku, pokud je směrodatná odchylka 13.

Řešení:

Vzhledem k tomu,

• Johnovo skóre testu, x = 93
• Průměr, μ = 68
• Směrodatná odchylka, ơ = 13

Proto lze z-skóre pro Johnovo skóre testu vypočítat pomocí výše uvedeného vzorce jako,

Z = (93 - 68) / 13

Z skóre bude -

Z skóre = 1,92

Proto je Johnovo skóre Ztest 1,92 směrodatná odchylka nad průměrným skóre třídy, což znamená, že 97,26% třídy (49 studentů) získalo méně než John.

Příklad č. 2

Vezměme si další podrobný příklad 30 studentů (protože z-test není vhodný pro méně než 30 datových bodů), kteří se zúčastnili třídního testu. Určete skóre z-testu pro 4. studenta na základě známek známených studenty ze 100 - 55, 67, 84, 65, 59, 68, 77, 95, 88, 78, 53, 81, 73, 66 , 65, 52, 54, 83, 86, 94, 85, 72, 62, 64, 74, 82, 58, 57, 51, 91.

Řešení:

Vzhledem k tomu,

• x = 65,
• 4. student skóroval = 65,
• Počet datových bodů, N = 30.

Průměr = (55 + 67 + 84 + 65 + 59 + 68 + 77 + 95 + 88 + 78 + 53 + 81 + 73 + 66 + 65 + 52 + 54 + 83 + 86 + 94 + 85 + 72 + 62 + 64 + 74 + 82 + 58 + 57 + 51 + 91) / 30

Průměr = 71,30

Nyní lze směrodatnou odchylku vypočítat pomocí vzorce uvedeného níže,

ơ = 13,44

Proto lze Z-skóre 4. studenta vypočítat pomocí výše uvedeného vzorce jako,

Z = (x - x) / s

• Z = (65–30) / 13,44
• Z = -0,47

Skóre 4. studenta je tedy 0,47 směrodatná odchylka pod průměrným skóre třídy, což znamená, že 31,92% třídy (10 studentů) skórovalo méně než 4. student podle tabulky z-skóre.

Skóre Z v aplikaci Excel (s šablonou Excel)

Nyní si vezmeme případ uvedený v příkladu 2, abychom ilustrovali koncept z-skóre v šabloně aplikace Excel níže.

Níže jsou uvedeny údaje pro výpočet Z skóre

Podrobný výpočet statistik testu vzorce Z Score Formula najdete v níže uvedeném listu aplikace Excel.

Relevance a použití

Z hlediska testování hypotéz je z-skóre velmi důležitým konceptem, který je třeba pochopit, protože se používá k testování, zda statistika testu spadá do přijatelného rozsahu hodnoty. Z-skóre se také používá ke standardizaci dat před analýzou, výpočtu pravděpodobnosti skóre nebo porovnání dvou nebo více datových bodů, které jsou z různých normálních distribucí. Při správném použití z-skóre napříč poli existuje různorodé použití.