seychellesartprojects.org

Vzorec pro výpočet regrese

Regresní vzorec se používá k posouzení vztahu mezi závislou a nezávislou proměnnou a ke zjištění, jak ovlivňuje závislou proměnnou na změnu nezávislé proměnné a je reprezentován rovnicí Y se rovná aX plus b, kde Y je závislá proměnná, a je sklon regresní rovnice, x je nezávislá proměnná ab je konstantní.

Regresní analýza široce používané statistické metody k odhadu vztahů mezi jednou nebo více nezávislými proměnnými a závislými proměnnými. Regrese je mocný nástroj, protože se používá k posouzení síly vztahu mezi dvěma nebo více proměnnými a poté by se použila k modelování vztahu mezi těmito proměnnými v budoucnu.

Y = a + bX + ∈

Kde:

• Y - je závislá proměnná
• X - je nezávislá (vysvětlující) proměnná
• a - je zachycení
• b - je sklon
• ∈ - a je zbytkový (chyba)

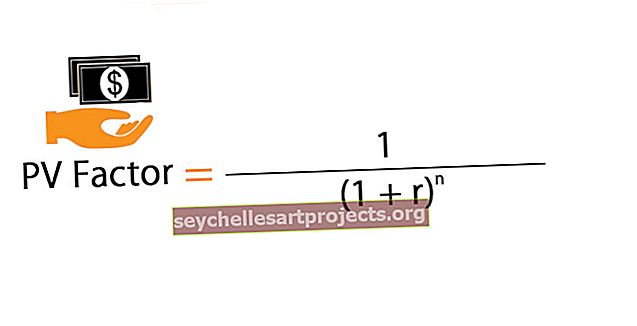
Vzorec pro přechod „a“ a sklon „b“ lze vypočítat níže.

a = (Σy) (Σx2) - (Σx) (Σxy) / n (Σx2) - (Σx) 2 b = n  (Σxy) - (Σx) (Σy)  / n (Σx2) - (Σx) 2

Vysvětlení

Regresní analýza, jak již bylo zmíněno dříve, se hlavně používá k nalezení rovnic, které budou odpovídat datům. Lineární analýza je jedním typem regresní analýzy. Rovnice pro přímku je y = a + bX. Y je závislá proměnná ve vzorci, který se pokouší předpovědět, jaká bude budoucí hodnota, pokud se X změní nezávislá proměnná o určitou hodnotu. „A“ ve vzorci je intercept, což je ta hodnota, která zůstane pevná bez ohledu na změny nezávislé proměnné a termín „b“ ve vzorci je sklon, který značí, kolik proměnné je závislou proměnnou na nezávislé proměnné.

Příklady

Tuto šablonu Regrese Formula Excel si můžete stáhnout zde - Šablona Regrese Formula Excel

Příklad č. 1

Zvažte následující dvě proměnné xay, je třeba provést výpočet regrese.

Řešení:

Pomocí výše uvedeného vzorce můžeme provést výpočet lineární regrese v aplikaci Excel následujícím způsobem.

Máme všechny hodnoty ve výše uvedené tabulce s n = 5.

Nyní nejprve vypočítáme průsečík a sklon pro regresi.

Výpočet Intercept je následující,

a = (628,33 * 88 017,46) - (519,89 * 106 206,14) / 5 * 88 017,46 - (519,89) 2

a = 0,52

Výpočet sklonu je následující,

b = (5 * 106,206,14) - (519,89 * 628,33) / (5 * 88,017,46) - (519,89) 2

b = 1,20

Pojďme nyní zadat hodnoty do regresního vzorce, abychom získali regresi.

Proto je regresní přímka Y = 0,52 + 1,20 * X 

Příklad č. 2

Indická státní banka nedávno zavedla novou politiku propojení úrokové sazby spořicího účtu s úrokovou sazbou Repo a auditor indické státní banky chce provést nezávislou analýzu rozhodnutí banky o změnách úrokových sazeb, ať už se jedná o změny, kdykoli došlo ke změnám v repo kurzu. Následuje přehled repo sazby a úrokové sazby spořicího účtu banky, které v těchto měsících převládaly, jsou uvedeny níže.

Auditor státní banky vás oslovil, abyste provedli analýzu a představili ji na příštím setkání. Použijte regresní vzorec a určete, zda se sazba banky změnila, kdy a kdy byla změněna repo sazba?

Řešení:

Pomocí výše diskutovaného vzorce můžeme provést výpočet lineární regrese v aplikaci Excel. Zacházení s repo sazbou jako s nezávislou proměnnou, tj. X, a zacházení s bankovní sazbou jako se závislou proměnnou, jako s Y.

Máme všechny hodnoty ve výše uvedené tabulce s n = 6.

Nyní nejprve vypočítáme průsečík a sklon pro regresi.

Výpočet Intercept je následující,

a = (24,17 * 237,69) - (37,75 * 152,06) / 6 * 237,69 - (37,75) 2

a = 4,28

Výpočet sklonu je následující,

b = (6 * 152,06) - (37,75 * 24,17) / 6 * 237,69 - (37,75) 2

b = -0,04

Pojďme nyní zadat hodnoty do vzorce, abychom dospěli k obrázku.

Proto je regresní přímka Y = 4,28 - 0,04 * X

Analýza: Zdá se, že indická státní banka skutečně dodržuje pravidlo spojování své míry úspor s repo sazbou, protože existuje určitá hodnota sklonu, která signalizuje vztah mezi repo sazbou a sazbou spořicího účtu banky.

Příklad č. 3

Laboratoř ABC provádí výzkum výšky a hmotnosti a chtěla vědět, jestli existuje nějaký vztah, jako když se zvyšuje výška, váha se také zvýší. Shromáždili vzorek 1000 lidí pro každou z kategorií a přišli s průměrnou výškou v této skupině.

Níže jsou uvedeny podrobnosti, které shromáždili.

Je od vás požadováno, abyste provedli výpočet regrese a dospěli k závěru, že takový vztah existuje.

Řešení:

Pomocí výše diskutovaného vzorce můžeme provést výpočet lineární regrese v aplikaci Excel. Zacházení s výškou jako s nezávislou proměnnou, tj. X, a s hmotností jako se závislou proměnnou, jako s Y.

Máme všechny hodnoty ve výše uvedené tabulce s n = 6

Nyní nejprve vypočítáme průsečík a sklon pro regresi.

Výpočet Intercept je následující,

a = (350 * 120 834) - (850 * 49 553) / 6 * 120 834 - (850) 2

a = 68,63

Výpočet sklonu je následující,

b = (6 * 49 553) - (850 * 350) / 6 * 120 834 - (850) 2

b = -0,07

Pojďme nyní zadat hodnoty do vzorce, abychom dospěli k obrázku.

Proto je regresní přímka Y = 68,63 - 0,07 * X

Analýza: Ukazuje se, že mezi výškou a hmotností existuje významný, velmi malý vztah, protože sklon je velmi nízký.

Relevance a použití vzorce regrese

Když korelační koeficient zobrazuje, že data mohou předpovídat budoucí výsledky, a spolu s tím se zdá, že bodový graf stejné datové sady tvoří lineární nebo přímku, pak lze použít jednoduchou lineární regresi pomocí nejvhodnějšího hledání prediktivní hodnotová nebo prediktivní funkce. Regresní analýza má mnoho aplikací v oblasti financí, jak se používá v CAPM, což je model oceňování kapitálových aktiv a metoda ve financích. Lze jej použít k předpovědi příjmů a výdajů firmy.