seychellesartprojects.org

Jaká je budoucí hodnota splatné anuity?

Budoucí hodnota splatné anuity je hodnota částky, která má být přijata v budoucnu, kdy je každá platba provedena na začátku každého období a vzorcem pro její výpočet je částka každé anuitní splátky vynásobená úrokovou sazbou na počet období minus jedno, které se dělí úrokovou sazbou a celá se vynásobí jednou plus úrokovou sazbou.

Budoucí hodnota vzorce splatného anuity

Matematicky je reprezentován jako,

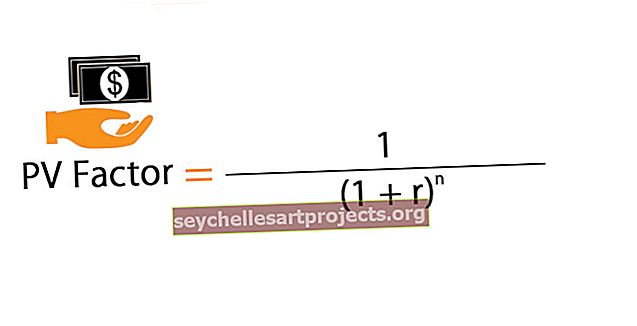
FVA _splatnost = P * [(1 + r) n - 1] * (1 + r) / r

kde FVA _Vzhledem = budoucí hodnota anuity náležité

• P = Periodická platba
• n = počet období
• r = efektivní úroková sazba

Jak vypočítat? (Krok za krokem)

• Krok 1: Nejprve zjistěte platby, které se mají platit v každém období. Pamatujte, že výše uvedený vzorec je použitelný pouze v případě stejných pravidelných plateb. Označuje ho P.
• Krok 2: Dále zjistěte úrokovou sazbu, která má být účtována, na základě převládající tržní sazby. Jedná se o úrokovou sazbu, kterou má investor obdržet, pokud jsou peníze investovány na trhu. Chcete-li získat efektivní úrokovou sazbu, vydělte anualizovanou úrokovou sazbu počtem pravidelných plateb za rok. Označuje se řek r = anualizovaná úroková sazba / počet pravidelných plateb za rok
• Krok 3: Dále se celkový počet období vypočítá vynásobením počtu pravidelných plateb za rok a počtu let. Označuje se nie n = počet let * počet pravidelných plateb za rok
• Krok 4: Nakonec se budoucí hodnota splatné anuity vypočítá na základě pravidelných plateb (krok 1), efektivní úrokové míry (krok 2) a počtu období (krok 3), jak je uvedeno výše.

Příklady

Tuto budoucí hodnotu šablony splatnosti anuity si můžete stáhnout zde - šablona budoucnosti budoucí splatnosti anuity

Příklad č. 1

Vezměme si příklad Johna Doea, který plánuje na začátku každého roku vložit 5 000 dolarů na příštích sedm let, aby ušetřil dostatek peněz na vzdělání své dcery. Určete částku, kterou bude mít John Doe na konci sedmi let. Upozorňujeme, že aktuální úroková sazba na trhu je 5%.

Vypočítejte FV anuity splatné pro Periodickou platbu pomocí výše uvedených informací,

FV _splatnosti anuity  = P * [(1 + r) n - 1] * (1 + r) / r

= 5 000 $ * [(1 + 5%) 7 - 1] * (1 + 5%) / 5%

Budoucí hodnota splatné anuity bude -

= 42 745,54 $ ~ 42 746 $

Proto po sedmi letech bude mít John Doe 42 746 dolarů, které může utratit za vzdělání své dcery.

Příklad č. 2

Vezměme si další příklad Nixonových plánů nashromáždit dostatek peněz na jeho MBA. Rozhodne se vložit měsíční splátku 2 000 $ na další čtyři roky (začátek každého měsíce), aby mohl shromáždit požadované množství peněz. Podle vzdělávacího poradce bude Nixon vyžadovat 100 000 USD za MBA. Zkontrolujte, zda Nixonovy vklady budou financovat jeho plány na MBA vzhledem k tomu, že aktuální úroková sazba účtovaná bankou je 5%.

Vzhledem k tomu,

• Měsíční platba, P = 2 000 $
• Efektivní úroková sazba, r = 5% / 12 = 0,42%
• Počet období, n = 4 * 12 měsíců = 48 měsíců

Vypočítejte FV splatné anuity pro měsíční platbu pomocí výše uvedených informací,

= 2 000 $ * [(1 + 0,42%) 48 - 1] * (1 + 0,42%) / 0,42%

Budoucí hodnota měsíční platby bude -

FV _splatné anuity  = 106 471,56 USD ~ 106 472 USD

U plánovaných vkladů se tedy očekává, že Nixon bude mít 106 472 USD, což je více než částka (100 000 USD) požadovaná pro jeho MBA.

Relevance a použití

Budoucí hodnota anuity je dalším vyjádřením TVM, dnes přijaté peníze lze nyní investovat, které budou v průběhu času růst. Jednou z jeho pozoruhodných aplikací je výpočet pojistného pro životní pojištění. Rovněž nachází uplatnění při výpočtu penzijního fondu, kde měsíční příspěvek ze mzdy funguje jako periodická platba. Budoucí hodnota anuity roste na základě uvedené diskontní sazby, protože čím vyšší diskontní sazba, tím vyšší bude budoucí hodnota anuity.