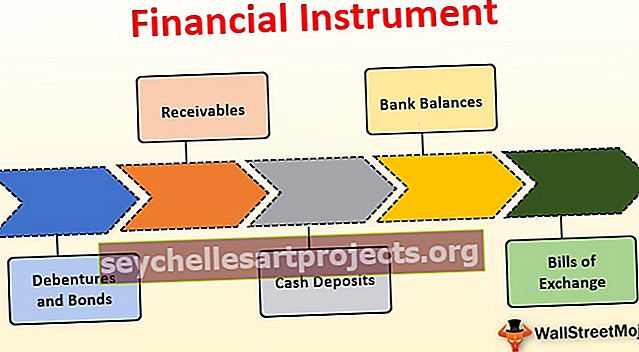
Zákon o snižování návratnosti (definice, příklady) S diagramem
Zákon o definici klesajících výnosů
Zákon klesajících výnosů uvádí, že další množství jediného výrobního faktoru bude mít za následek snížení mezní produkce. Zákon předpokládá, že další faktory budou konstantní. To znamená, že pokud X produkuje Y, bude mít bod, když přidání více množství X nepomůže v marginálním zvýšení množství Y.

Ve výše uvedeném grafu zákona klesajících výnosů, jak faktor X stoupá z 1 jednotky na 2 jednotky, počet Y roste. Ale jak množství X stoupá dále k P, produkce předpokládá klesající rychlost až do Yp. Toto popisuje zákon výše. Dalším znatelným aspektem je, že nastane okamžik, kdy další zvýšení jednotek X sníží pouze produkci Y. Zvyšování vstupu tedy neovlivňuje pouze okrajový produkt, ale také celkový produkt. Tento zákon je většinou použitelný v produkčním prostředí.
Součásti zákona o snižování návratnosti
Z definice zákona o snižování výnosů existují tři složky.

- Výrobní faktor - Jakýkoli vstup, který generuje požadované množství výstupu. Pokud jde o zákon o snižování výnosů, zohledňuje se vždy pouze jeden faktor.
- Okrajový produkt - S každým dalším vstupem se přírůstek celkového produktu označuje jako okrajový produkt. Ve výše uvedeném grafu je Y 2 -Y 1 mezním produktem.
- Celkový produkt - Když je vstup aplikován prostřednictvím procesu, výsledkem nebo výsledkem jako agregovaná míra je celkový produkt.
Předpoklady zákona o snižování mezních výnosů
- Zákon se používá většinou při zohlednění scénáře krátkodobé produkce. Je to proto, že princip spočívá v udržování všech ostatních výrobních faktorů jako konstantních, kromě faktoru použitého ke korelaci s výstupem. To není možné v dlouhodobém pohledu na produkci.
- Vstup a procesy by měly být nezávislé na technologických aspektech, protože technologie může hrát svoji roli při zlepšování efektivity výroby.
Příklady zákona o snižování mezních výnosů
Níže jsou uvedeny příklady zákona o snižování výnosů.
Tento zákon o snižování výnosů Excel si můžete stáhnout zde - Zákon o snižování výnosů Excel šablonyPříklad č. 1
Předpokládejme, že továrna produkuje určité zboží dané následující rovnicí:
Q = -L3 + 27L2 + 15L
Kde,
Q je množství produkce
L je vstup z hlediska práce
Popište, zda platí zákon o snižování výnosů, pokud ano, jak?
Řešení:
Abychom zkontrolovali použitelnost tohoto zákona, budeme kvantifikovat jednotky výroby za předpokladu různých hodnot vstupů práce.

Hodnoty Q a L zakreslíme do grafu pro analýzu. Osa Y představuje Produkt (celkový a okrajový). Osa x představuje jednotky práce.

Ve výše uvedeném zákonu klesajícího grafu návratnosti jsou pro zákon rozhodující dva body:
- Bod A - omezující mezní produkt a
- Bod B - omezující celkový produkt.
Za zmínku stojí následující body:
Můžeme tento produkční graf rozdělit do 2 fází s ohledem na mezní výstup.
- Jak se zvyšuje pracovní síla, zvyšuje se také mezní produkt před počtem pracovníků, L = 9. Toto je fáze zvyšování návratnosti.
- Mezní produkt produkovaný 11. jednotkou práce je menší než 10. Tím začíná fáze klesajícího výnosu.
Celkový produkt, tj. Množství Q, neklesá před zaměstnáním 20. pracovníka. Je zřejmé, že mezní produkt odtud vstupuje do fáze negativních výnosů.
Továrna může zaměstnávat 9 pracovníků, aby udržovala mezní produkt na rostoucí rychlosti. Může však přidat až 19 pracovníků, než zaznamená pokles celkového produktu.
Příklad č. 2
Farmář vlastní malé pšeničné pole. Začne obdělávat svou půdu s jedním dělníkem. Postupně ji zvyšuje na šest dělníků, jen aby zjistil, že jeho produkce pšenice se proporcionálně nezvýšila. Pomozte farmáři při analýze optimální požadované pracovní síly.

Řešení:
Pouhým pohledem na produkci pšenice oproti použité práci můžeme říci, že mezní produkce klesá s každou další nasazenou prací. Pokud odvodíme mezní produkt a představíme jej zemědělci, bude vypadat takto:

To ukazuje, že mezní produkt se zvyšuje před přijetím služeb 4. dělníka. Poté hraniční produkt klesá.
Farmář by tedy měl optimalizovat produkci pšenice se 3 dělníky na svém poli.
Na druhou stranu může maximalizovat svůj celkový produkt pokračováním zvyšování počtu dělníků. To však přichází za cenu sníženého mezního výkonu.
Tyto dva příklady z dobrého stadia, ve kterém se můžeme podívat na výhody a omezení „zákona klesajících výnosů“.
Výhody zákona o snižování návratnosti
- Zákon klesajících výnosů pomáhá managementu maximalizovat práci (jako v příkladech 1 a 2 výše) a dalších výrobních faktorech na optimální úroveň.
- Tato teorie také pomáhá zvyšovat efektivitu produkce minimalizací výrobních nákladů, jak je patrné z případu chovatele pšenice.
Omezení zákona o snižování návratnosti
- I když je tento zákon užitečný ve výrobních činnostech, nelze jej použít ve všech formách výroby. Omezení nastává, když jsou výrobní faktory méně přirozené, a proto je univerzální použití obtížné. Tento zákon se většinou uplatňuje v zemědělských scénářích.
- Zákon předpokládá, že všechny jednotky jednoho výrobního faktoru musí být totožné. To však obvykle není praktické a v aplikaci se stává překážkou. V našich výše uvedených příkladech se práce stává specifickým vstupem, ostatní faktory zůstávají konstantní.
Závěr
Zákon klesajících výnosů je v teorii výroby užitečným konceptem. Zákon lze rozdělit do tří fází - zvyšování výnosů, snižování výnosů a negativní výnosy. Produkční průmysl, a zejména zemědělství, nachází obrovské uplatnění tohoto zákona. Producenti se ptají, kde pracovat na grafu mezního produktu, protože první fáze popisuje nedostatečně využitou kapacitu a třetí fáze je o příliš nevyužívaných vstupech. Proto je dosažení optimální kapacity důvodem tohoto zákona.