seychellesartprojects.org

Co je to faktor slevy?

Diskontní faktor je váhový faktor, který se nejčastěji používá k nalezení současné hodnoty budoucích peněžních toků a vypočítá se přidáním diskontní sazby k jedné, která se poté zvýší na zápornou sílu řady období.

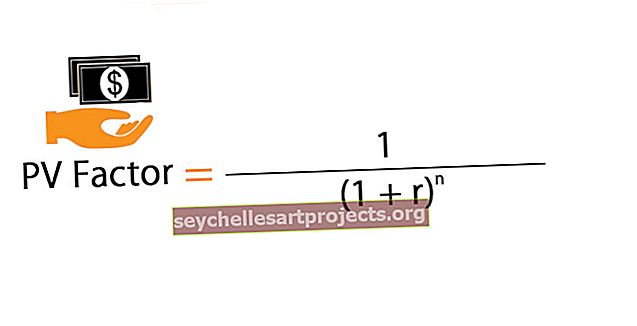
Vzorec faktoru slevy

Matematicky je to znázorněno níže,

DF = (1 + (i / n) ) -n * t

kde,

• i = diskontní sazba
• t = počet let
• n = počet slučovacích období diskontní sazby za rok

V případě spojitého vzorce se rovnice upraví níže,

DF = ei * t

Výpočet (krok za krokem)

Lze jej vypočítat pomocí následujících kroků:

• Krok 1: Nejprve na základě informací o trhu zjistěte diskontní sazbu pro podobný druh investice. Diskontní sazba je anualizovaná úroková sazba a je označena písmenem „i“.
• Krok 2: Nyní určete, jak dlouho zůstanou peníze investovány, tj. Doba trvání investice z hlediska počtu let. Počet let je označen písmenem „t“.
• Krok 3: Nyní zjistěte počet složených období diskontní sazby za rok. Sčítání může být čtvrtletní, pololetní, roční atd. Počet sloučených období diskontní sazby za rok je označen písmenem „ n“. (Tento krok není vyžadován pro průběžné skládání)
• Krok 4: Nakonec v případě diskrétního složení lze vypočítat pomocí následujícího vzorce jako,

DF = (1 + (i / n) ) -n * t 

Na druhou stranu, v případě spojitého skládání to lze vypočítat pomocí následujícího vzorce jako,

DF = ei * t

Příklady (s šablonou Excel)

Tuto šablonu pro výpočet faktoru slevy Excel si můžete stáhnout zde - Šablona aplikace Excel pro faktor slevy

Příklad č. 1

Vezměme si příklad, kdy se diskontní faktor počítá na dva roky se diskontní sazbou 12%. Složení se provádí:

1. Kontinuální
2. Denně
3. Měsíční
4. Čtvrtletní
5. Pololetní
6. Roční

Vzhledem k tomu, i = 12%, t = 2 roky

# 1 - Kontinuální skládání

Vzorec = e-12% * 2

• DF = 0,7866

# 2 - denní složení

Od denního složení tedy n = 365

= (1 + (12% / 365)) - 365 * 2

= 0,7867

# 3 - Měsíční složení

Od měsíčního složení tedy n = 12

Výpočet DF se provádí pomocí výše uvedeného vzorce jako,

= (1 + (12% / 12)) - 12 * 2

= 0,7876

# 4 - Čtvrtletní složení

Od čtvrtletního složení tedy n = 4

Výpočet DF se provádí pomocí výše uvedeného vzorce jako,

= (1 + (12% / 4)) - 4 * 2

= 0,7894

# 5 - Pololetní složení

Od pololetního složení tedy n = 2

= (1 + (12% / 2)) - 2 * 2

= 0,792

# 6 - Roční složení

Od ročního složení, tedy n = 1,

Výpočet DF se provádí pomocí výše uvedeného vzorce jako,

= (1 + (12% / 1)) - 1 * 2

= 0,7972

Diskontní faktor pro různá slučovací období tedy bude -

Grafické znázornění výše uvedené tabulky bude následující -

Výše uvedený příklad ukazuje, že vzorec závisí nejen na míře diskontu a držbě investice, ale také na tom, kolikrát se sazba během roku stane.

Příklad č. 2

Vezměme si příklad, kde se diskontní faktor počítá od roku 1 do roku 5 se diskontní sazbou 10%.

Proto bude výpočet DF od 1. roku do 5. roku následující:

• DF pro rok 1 = (1 + 10%) -1  = 0,9091
• DF pro 2. rok = (1 + 10%) -2  = 0,8264
• DF pro rok 3 = (1 + 10%) -3  = 0,7513
• DF pro 4. rok = (1 + 10%) -4   = 0,6830
• DF pro 5. rok = (1 + 10%) -5   = 0,6209

Proto je DF roku 1 až roku 5 zobrazen na následujícím obrázku -

Výše uvedený příklad zachycuje závislost společnosti DF na držbě investice.

Kalkulátor faktoru slevy

Diskontní sazba
Počet složených období
Počet let
Vzorec faktoru slevy

Vzorec faktoru slevy	1 + (diskontní sazba / počet složených období) - počet složených období * počet let
	1 + (0/0) - 0 * 0 =	0

Použití a relevance

Pochopení tohoto diskontního faktoru je velmi důležité, protože zachycuje účinky složení na každé časové období, což nakonec pomůže při výpočtu diskontovaných peněžních toků. Koncept spočívá v tom, že se časem snižuje, jak se v průběhu času buduje účinek skládání diskontní sazby. Jako takový je velmi důležitou součástí časové hodnoty peněz.

Jedná se o desítkové vyjádření použité v časové hodnotě peněz pro peněžní tok. K určení diskontního faktoru pro peněžní tok je třeba posoudit nejvyšší úrokovou sazbu, jakou lze při investici podobné povahy získat. V důsledku toho mohou investoři tento faktor využít při převodu hodnoty budoucích výnosů z investic na současnou hodnotu v dolarech.