Vzorec meze chyby | Výpočet krok za krokem (s příklady)
Co je to marže chyby?
Margin of Error je statistický výraz, který se používá k určení procentního bodu, o který se dosažený výsledek bude lišit od hodnoty skutečné populace, a vypočítá se vydělením standardní odchylky populace velikostí vzorku a nakonec vynásobením výslednice s kritickým faktorem.
Vyšší chyba naznačuje, že existuje velká šance, že výsledek nahlášeného vzorku nemusí být skutečným odrazem celé populace.
Vzorec chyby
Vzorec pro hranici chyby se vypočítá vynásobením kritického faktoru (pro určitou úroveň spolehlivosti) se směrodatnou odchylkou populace a poté se výsledek vydělí druhou odmocninou počtu pozorování ve vzorku.
Matematicky je reprezentován jako,
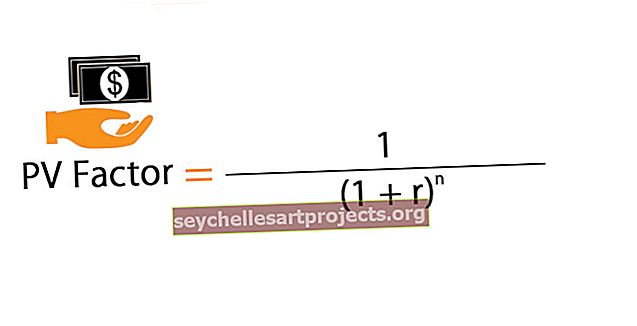
Marže chyby = Z * ơ / √n
kde
- z = kritický faktor
- ơ = směrodatná odchylka populace
- n = velikost vzorku
Výpočet rozpětí chyby (krok za krokem)
- Krok 1: Nejprve shromážděte statistická pozorování a vytvořte soubor dat nazývaný populace. Nyní vypočítejte průměr populace. Dále vypočítejte směrodatnou odchylku populace na základě každého pozorování, průměrné hodnoty populace a počet pozorování populace, jak je uvedeno níže.

- Krok 2: Dále určete počet pozorování ve vzorku a je označen n. Nezapomeňte, že velikost vzorku je menší než rovná celkové populaci, tj. N ≤ N.
- Krok 3: Dále určete kritický faktor nebo z-skóre na základě požadované úrovně spolehlivosti a je označeno z.
- Krok 4: Dále se nakonec vypočítá chyba rozpětí vynásobením kritického faktoru pro požadovanou úroveň spolehlivosti a směrodatnou odchylku populace a poté se výsledek vydělí druhou odmocninou velikosti vzorku, jak je uvedeno výše.
Příklad
Tuto šablonu Excel Margin of Error Formula si můžete stáhnout zde - Margin of Error Formula Excel Template
Vezměme si příklad 900 studentů, kteří byli součástí průzkumu, a bylo zjištěno, že průměrná GPA populace byla 2,7 se standardní směrodatnou odchylkou 0,4. Vypočítejte míru chyby pro
- 90% úroveň spolehlivosti
- 95% úroveň spolehlivosti
- 98% úroveň spolehlivosti
- 99% úroveň spolehlivosti
Pro výpočet použijeme následující údaje.

Pro 90% úroveň spolehlivosti
Pro 90% hladinu spolehlivosti je kritický faktor nebo hodnota z 1,645, tj. Z = 1,645
Proto lze chybu na 90% úrovni spolehlivosti provést pomocí vzorce nad,

- = 1,645 * 0,4 / √900
Chyba okraje při 90% úrovni spolehlivosti bude-

- Chyba = 0,0219
Pro 95% úroveň spolehlivosti
Pro 95% hladinu spolehlivosti je kritický faktor nebo hodnota z 1,96, tj. Z = 1,96
Výpočet rozpětí chyby na 95% úrovni spolehlivosti lze tedy provést pomocí výše uvedeného vzorce jako,

- = 1,96 * 0,4 / √900
Chyba marže na 95% spolehlivosti bude-

- Chyba = 0,0261
Pro 98% úroveň spolehlivosti
Pro úroveň spolehlivosti 98% je kritický faktor nebo hodnota z 2,33, tj. Z = 2,33
Výpočet míry chyby na úrovni spolehlivosti 98% lze tedy provést pomocí výše uvedeného vzorce jako,

- = 2,33 * 0,4 / √900
Chyba okraje na 98% úrovni spolehlivosti bude-

- Chyba = 0,0311
Proto je chyba vzorku na 98% úrovni spolehlivosti 0,0311.
Pro 99% úroveň spolehlivosti
Pro hladinu spolehlivosti 99% je kritický faktor nebo hodnota z 2,58, tj. Z = 2,58
Výpočet marže na 99% úrovni spolehlivosti lze tedy provést pomocí výše uvedeného vzorce jako,

- = 2,58 * 0,4 / √900
Chyba okraje na 99% úrovni spolehlivosti bude-

- Chyba = 0,0344
V důsledku toho lze vidět, že chyba vzorku se zvyšuje se zvyšováním úrovně spolehlivosti.
Kalkulačka meze chyby
Můžete použít následující kalkulačku.
| z | |
| σ | |
| n | |
| Vzorec odchylky chyby = | |
| Vzorec odchylky chyby = |
|
|||||||||
|
Relevance a použití
Je velmi důležité pochopit tento koncept, protože naznačuje, do jaké míry lze očekávat, že výsledky průzkumu skutečně odrážejí skutečný pohled na celkovou populaci. Je třeba mít na paměti, že průzkum se provádí s využitím menší skupiny lidí (také známých jako respondenti průzkumu), která představuje mnohem větší populaci (známou také jako cílový trh). Rovnici meze chyby lze chápat jako způsob měření účinnosti průzkumu. Vyšší marže naznačuje, že výsledky průzkumu se mohou odchýlit od skutečných pohledů na celkovou populaci. Na druhou stranu menší rozpětí naznačuje, že výsledky se blíží skutečnému odrazu celkové populace, což zvyšuje důvěru v průzkum.